Difference between revisions of "Legacy Power Systems"

From StarMade Wiki
(Opening paragraph clarified/added references to Power Auxiliaries. Fixed headings for Power Reactor formulas, too.)
(Improving clarity of article. Future plans: removal of most references to outdated "cubic" reactors.)
Line 11: Line 11:
  
 
==Power Reactor Rules==
 
==Power Reactor Rules==
−
[[Power Reactor Module|Power Reactors]] have a somewhat complex set of rules associated with them when it comes to creating efficient or compact power systems.  This comes from how their power output is calculated, which is not simply by adding up the blocks and multiplying them by some power factor. There are two separate formulas for this: one which will find the regeneration of a single group of Power Reactors on a ship, and another which deals with multiple separate groupings of Power Reactors.
+
[[Power Reactor Module|Power Reactors]] have some relatively complex rules governing their power output, especially if one is concerned about efficiency (either in terms of power per block, or power per volume). Two separate formulas are used: one which deals with the output of a single group of reactors (which is only used when the ship has exactly one reactor group), and one which is used to calculate the total output of multiple separate groups on a ship.
  
 
===Single Group Formula===
 
===Single Group Formula===
Line 28: Line 28:
  
  
−
'''GroupPower''' is fairly straightforward, as it is the simple sum of the other two pieces.   
+
'''GroupPower''' is the sum of the following values.   
  
−
'''BlockPower''' is the amount of power contributed directly by the [[Power Reactor Module]]s in the group, which is just 25e per module.
+
'''BlockPower''' is the base power per second per block of [[Power Reactor Module|Power Reactors]]: 25e/sec/block.
  
−
'''SizePower''' is the amount of power contributed by the '''size''' of the group, and is only dependent on '''SumOfDimensions''' which is the sum of the dimensions of the smallest bounding box which can encompass the entire group.  Because SumOfDimensions is a plain sum, a 3x3x3 box, 1x1x7 box and a 2x2x5 box are the same (9) for the purposes of this part of the equation.  This is the part of the equation which is most important when considering how to maximize a group of reactors because SizePower is a power function, which means that each successive incremental increase in the value of SumOfDimensions gives much greater benefits than the next lower value.  
+
SizePower is an extra power value dependent on SumOfDimensions: the sum of dimensions of the minimum bounding box for a given reactor group.  SumOfDimensions, of course, is not dependent on aspect ratio: a 3x3x3, 1x1x7, and 2x2x5 bounding box all have a SumOfDimensions of 9.  SizePower is of the greatest importance to efficient reactor design as it is an exponential function, and every successive increase in SumOfDimensions has greater value than the last.  
  
−
Note that SizePower caps out at 2,000,000e.  Also note that for multiple reactor groups, the above formula is modified, and results in a diminishing return. Total Power of a ship is not the sum of the Group Power of each group. See the [[#Power Reactor Advanced Analysis|Advanced Analysis]] section for a more detailed explanation of the equation.
+
Note that SizePower has a maximum value of 2,000,000e/sec, and suffers from diminishing returns as it approaches this value.  Also note that for multiple reactor groups, the above formula is modified, and results in a diminishing return to TotalPower. TotalPower of an entity is not the sum of the GroupPower of each group. See the [[#Power Reactor Advanced Analysis|Advanced Analysis]] section for a more detailed explanation of the equation.
  
 
Here are some examples of power reactor groups and how their power outputs are calculated.
 
Here are some examples of power reactor groups and how their power outputs are calculated.
Line 46: Line 46:
 
===Multiple Group Formula===
 
===Multiple Group Formula===
  
−
When there is only one power reactor block group in or on an entity, the GroupPower and the total power of the entity is identical. However, when there is more than one group, the total power provided to a ship, station or planet is ''not'' the sum of the GroupPower of all groups. Rather,  '''TotalPower''' of an entity with multiple power reactor groups is subject to diminishing returns, and is given by the following formula:
+
When there is only one power reactor group on an entity, the GroupPower of that reactor is equal to the total power regen of the entity. However, when there is more than one group, the total power regen of the entity is ''not'' the sum of the GroupPower of all groups. Rather,  '''TotalPower''' of an entity with multiple power reactor groups is subject to diminishing returns, and is given by the following formula:
  
 
<tt style="font-size: large">'''TotalPower''' = BlockPower + GroupSumSizePower</tt>
 
<tt style="font-size: large">'''TotalPower''' = BlockPower + GroupSumSizePower</tt>
Line 63: Line 63:
  
  
−
To understand the relationship between SizePower, BlockPower and TotalPower, consider a 3x3x3 space in which to place a set of reactor modules.  Below are three layouts in this 3x3 space.  Note that values are rounded which may lead to small apparent discrepancies.
+
To understand the relationship between SizePower, BlockPower and TotalPower, consider a 3x3x3 space in which to place a set of reactor modules.  Below are three layouts in this 3x3 space.  Note that all values displayed around rounded.
  
 
<gallery mode="traditional" widths=300px heights=300px perrow=3 caption="Example 3x3x3 layouts with power values">
 
<gallery mode="traditional" widths=300px heights=300px perrow=3 caption="Example 3x3x3 layouts with power values">
Line 71: Line 71:
 
</gallery>
 
</gallery>
  
−
Notice that the first and second versions have the same SizePower, as SizePower depends only on the dimensions of the group and not the number of blocks.  The first of course produces more total power than the second because it has more blocks and each only has a single group, but SizePower still contributes more to the total than the number of blocks does.  Then look at the third version, which has the same dimensions but two groups instead of one.  The SizePower is twice that of the other two because there are two groups and because SizePower counts for much more than BlockPower the TotalPower of the third version is much higher than the first one, in spite of only having half as many blocks in it (and thus a lower BlockPower).
+
Notice that the first and second versions have the same SizePower, as SizePower depends only on the dimensions of the group's bounding box, and not the number of blocks.  The first produces more power because it has a greater BlockPower and the same SizePower, but SizePower still contributes more to TotalPower than BlockPower does.  Then look at the third version, which has the same dimensions but two groups instead of one.  The SizePower is twice that of the other two because there are two groups and because SizePower counts for much more than BlockPower. Because of this, the TotalPower of the third version is much higher than the first one, in spite of having almost half the BlockPower.
  
−
Please note that with the very small groups in the cubic structure above, the diminishing returns of TotalPower with multiple groups is not noticeable with such small power output rounded to a whole number.  But note the case of a group of 1000 power reactors in one group, 500 in one group, and finally a third case of two groups of 500, for a total of 1000 blocks.
+
Please note that with very small groups as seen above, the diminishing returns of TotalPower with multiple groups is not noticeable due to rounding of such small numbers.  However, note the following examples:
  
−
# 1000 in one group: GroupPower/TotalPower = 1647409.7 e/sec
+
# 1000 blocks in one group: TotalPower = 1,647,409.7 e/sec
−
# 500 in one group: GroupPower/TotalPower = 683737.4 e/sec
+
# 500 blocks in one group: TotalPower = 683,737.4 e/sec
−
# 1000 in two groups of 500: TotalPower = 1231567.2 e/sec, not the double of 683737.4.
+
# 1000 total blocks, in two groups of 500: TotalPower = 1,231,567.2 e/sec, not (2*683,737.4=1,367,474.8).
  
 
===Optimal layouts===
 
===Optimal layouts===
−
None of the examples above are optimal layouts for the cubic 3x3x3 volume, though the third version is getting close.  To create an optimal layout in a given space is rather complex, but it boils down to the following three rules:
+
None of the examples above are optimal layouts for the cubic 3x3x3 volume, though the third version is close.  To create an optimal layout in a given space is rather complex, but it boils down to the following three rules:
−
* Maximize the SumOfDimensions for each group, because this contributes the most to the power equation through SizePower.
+
* Maximize the SumOfDimensions for each group, because SizePower is the greatest contributor to TotalPower.
−
* Maximize the number of such groups in the space, because this allows you to take advantage of SizePower for each group
+
* Maximize the number of such groups in the space, because this allows you to take advantage of SizePower for each group.
−
* Minimize the number of empty spaces - that is, spaces which don't contain power reactor modules - without reducing the number of groups. When doing this, be mindful of the fact that a block in a group of its own is worth 140e/s, while a block added to an existing group is only worth 25e/s if it doesn't also add to the physical size of the group.
+
* Minimize the amount of space not used by reactor groups, without also decreasing the number of groups. It is relevant to note that a 1-block group produces 140e/sec, whereas adding that block to a group ''without'' it serving to increase SizePower will only add 25e/sec (from BlockPower) to that group's output.
  
 
The optimal layout for the 3x3x3 example above fills in as many spaces as possible in the cube without the two groups touching.  By filling in empty spaces of the third example above, we can increase the BlockPower of each group to 250e/s, and we are left with only 7 empty spaces (6 exterior and the block in the middle is omitted).  It looks like the following:
 
The optimal layout for the 3x3x3 example above fills in as many spaces as possible in the cube without the two groups touching.  By filling in empty spaces of the third example above, we can increase the BlockPower of each group to 250e/s, and we are left with only 7 empty spaces (6 exterior and the block in the middle is omitted).  It looks like the following:
Line 91: Line 91:
 
</gallery>
 
</gallery>
  
−
Once you have put in as many [[Power Reactor Module|Power Reactor Modules]] as you can into the space, you can fill the remaining spaces with any other module, except you should not use [[Power Capacitor|Power Capacitors]] because they can benefit from grouping as well, though it differs from power reactors. Using [[Shield Recharger]]s or [[Shield Capacitor|Shield Capacitors]] for this purpose is common.
+
Once the space is well packed with [[Power Reactor Module|Power Reactor Modules]] the remaining spaces can be filled with any other module. Bear in mind that blocks which benefit from being in physically contiguous groupings, such as [[Power Capacitor|Power Capacitors]] or [[Power Auxiliary|Power Auxiliaries]] do not make ideal fillers, as the gaps between reactors may not be contiguous, depending on reactor layout. Using [[Shield-Recharger|Shield-Rechargers]] or [[Shield Capacitor|Shield Capacitors]] is common, as they do not rely on being in a group.  
  
−
Layouts need not be cube-shaped to be optimal, even though this page uses them for examples. The above 3x3x3 example is the optimal '''cubic''' structure, for the most power that can be generated in the smallest cubic volume, but does not provide the most power that can be generated for the blocks used, which is 20.  The layout shape will typically be dictated by the ship or station dimensions. Keep in mind that since other shapes provide more power than a cubic volume, it is unlikely that a ship or station would be best served with a perfectly cubic power structure, even if the ship is itself a large cube.
+
Cubic layouts are often non-ideal for a given ship, and are an outdated academic excercize which saw use when these formulas were first being tested. The above 3x3x3 example is the optimal ''cubic'' structure, for the most power that can be generated in the given cubic volume, but does not provide the greatest power per second per block (the accepted measure of reactor efficiency) for the 20 blocks used.  Reactor layouts should be designed to fit the entity they are built for, in particular to maximise SizePower within the space available.
  
  
Line 100: Line 100:
 
</gallery>
 
</gallery>
  
−
Note that though not pictured above, a simple straight line of Power Reactor blocks is also a maximum-output layout as well.
+
Note that, though not pictured above, a straight line of Power Reactor blocks is also a maximum-efficiency layout for a given block count. This is because each block increases SumOfDimensions, ensuring the greatest possible SizePower for the group.
  
−
In the picture above, the first structure on the left uses the same number of cubes as the 3x3x3 cubic power structure shown in the lower middle, but generates almost twice the power at 3926.8e/s. For 20 blocks, this is the maximum power that can be generated. However, other shapes can also achieve the same box dimension sum as the first structure. Each of the other four structures on the upper deck in the picture above '''also''' generate the maximum power of 3926.8e/s. Thus it is likely for almost any ship volume that a custom, non-cubic reactor structure will generate more power than simply using an efficient cubic volume. Furthermore, the true cubic volume of all of the structures in the image above is actually '''20'''. In other words, each of the above structures have an identical impact on the internal volume of a given ship, which is to consume 20 blocks of the ship's total internal volume, but the 3x3x3 cubic shape only generates '''half''' of the other structure's power per second.  
+
In the picture above, the first structure on the left uses the same number of blocks as the 3x3x3 cubic power structure shown in the lower middle, but generates almost twice the power at 3926.8e/s. For 20 blocks, this is the maximum power that can be generated. However, other shapes can also achieve the same box dimension sum as the first structure. Each of the other four structures on the upper deck in the picture above ''also'' generate the maximum power of 3926.8e/s. Thus it is likely for almost any ship volume that a custom, non-cubic reactor structure will generate more power than simply using a compact cubic reactor. Furthermore, the true cubic volume of all of the structures in the image above is actually ''20''. In other words, each of the above structures have an identical impact on the internal volume of a given ship, which is to consume 20 blocks of the ship's total internal volume, but the 3x3x3 cubic shape only generates '''half''' of the other structure's power per second.  
  
−
The goal in design of a ship's power generation should be to both maximize the power reactor structure's box dimensions while also reserving large contiguous volumes within the ship for weapons and effects groups, functional areas like a core room, computer room, shuttle docking bay, or cargo hold, and usually some role-play areas, like a cockpit or command deck, medical facility, captain's quarters, corridors, elevators, etc. A cubic volume is not capable of fulfilling this goal.
+
The goal in design of a ship's power generation should be to both maximize every group's box dimensions (netting the greatest power per block efficiency) while also reserving large contiguous volumes within the ship for other systems, as well as rooms of both functional (core room and access paths) and non-functional nature. A cubic volume, although easy to fit into a ship, tends to have a relatively low power per block value, voiding the primary goal of efficient reactor design.
  
−
Taking these things into consideration, the process for designing an optimized power system for a ship is:
+
To restate the previously-noted conditions of efficient reactor design:
−
# Build the largest optimized group possible within the volume of the ship. An optimized group is one in which each added power reactor always increases the block dimensions of the group.
+
* Build the largest optimized group possible within the volume of the ship: ideally, every Power Reactor in the group will increase SumOfDimensions. Simply placing long lines or 3-axes crosses is common, due to the simplicity of the shapes.
−
# An allowed exception for the above rule would be, when following the inside of the hull from front to back, it might be necessary to go down before heading back up in order to go further to the back of the ship. (Some of the blocks won't increase the box-dimensions of the group, but they connect and make a contiguous group from front to back, so the group isn't optimal, but it is as close as possible while maximizing contiguous ship volume. Note that if a group consists of 100 blocks, but twenty of these blocks are connector blocks that do not increase the box-dimensions of the group, then this group should be considered as an 80-block system for purposes of calculating its SizePower, as the 20 connector blocks only add 25e/sec each, and do not increase the SizePower efficiency bonus.)
+
** An allowable exception to this is where a minimal number of redundant (non-SumOfDimensions-increasing blocks) will allow an even greater increase in SumOfDimensions: eg. taking a small detour around other systems to provide a non-negligible increase in SumOfDimensions after the detour.
−
# Once the first group is laid in, if needing more e/sec, lay in parallel, un-connected groups, extending along the first group as far as possible. In most cases, it is possible to build with symmetry, thus building at least two groups at a time.
+
* Once the first (and usually largest) group is placed, it is likely that more will be required to reach the desired e/sec output. Where possible, run separate groups along the same path as the primary group, ensuring that you do not connect them at any point (diagonal adjacency is usually preferable). Symmetry may prove useful in placing several groups.
−
# Finally,  even single reactors placed alone, unconnected, will yield 140e/sec, so filling in small pockets with single blocks is better than connecting them to existing groups if they do not also increase the box-dimensions of the group, in which case they only yield 25e/sec.
+
* Bear in mind that 1-block groups produce 140e/sec, compared to the 25e/sec that redundant blocks in a group will add. Fill gaps with small groups, rather than connecting large groups redundantly; the latter is likely to produce a loss in TotalPower.  
  
−
There is also a diminishing return as the e/sec of a ship approach 2 million e/sec. See the [[#Power Reactor Advanced Analysis|Advanced Analysis]] section  below.
+
There is also a diminishing return to GroupSumSizePower as it approaches 2,000,000e/sec. See the [[#Power Reactor Advanced Analysis|Advanced Analysis]] section  below.
  
  
Line 118: Line 118:
  
 
==Power Auxiliary Rules==
 
==Power Auxiliary Rules==
−
Power Auxiliaries fulfill a unique role, and should only be used once Power Reactor Modules have reached or surpassed their peak efficiency. They also provide a new element of risk to manage during ship design, as the chain reactions caused by destroying part of a Power Auxiliary group can be significant if not well mitigated.  
+
Power Auxiliaries add a new "auxiliary" power pool to a ship, which can be emptied into the main pool for emergency recharging, or used to provide a constant boost to power generation. They should only be used once Power Reactor Modules have reached or surpassed their peak efficiency. They also provide a new element of risk to manage during ship design, as the chain reactions caused by destroying part of a Power Auxiliary group can be significant if not well mitigated.  
 
{{main|Power Auxiliary}}
 
{{main|Power Auxiliary}}
  

Revision as of 23:22, 5 October 2016

This page describes the power generation and storage mechanisms in StarMade.

Power Generation and Storage Blocks

Power is generated using either Power Reactor Modules or Power Auxiliaries, although the latter is greatly preferable as a supplement to the former (when they have reached or surpassed their peak efficiency), not a replacement. Entities built from a Ship Core have an innate power regen rate of 1 power per second (commonly abbreviated as "e/sec"). Planets and Space Stations do not have this innate power generation. Ships also have a base power capacity of 50,000 energy (as with regeneration, planets and stations have no innate power capacity). Power capacity can be increased using Power Capacitors. All three types of power blocks are more efficient (in terms of power per second per block, or e/sec/block) when placed in particular configurations, as detailed in their sections below.

An important consideration is that all systems drain some amount of power from the ship's capacity, either at a constant rate for a period of time (passive effects, scanner and jump drive charging, or cloaking and jamming), or in instantaneous bursts of varying frequency (most weapons). If the instantaneous power cost of an action (eg. firing a large missile) is greater than the power capacity of the ship, the action will not occur, a "Power Failure" warning will appear below the targeting reticle (as well as a red "E" in a triangle, at the top of the screen), and no power will be drained for that action. In most situations, a ship should at least have sufficient capacity to fire one salvo of its alpha (high damage, long cooldown) weapons. Power capacity should usually also include leeway for power spikes caused by shield regeneration costs, thruster activation, and potentially even enemy EMP attacks (which can cause significant power drain if the attacking ship is focussed on such weaponry).

Power generation will ideally be greater than the maximum expected rate of power usage: failing this, there should be a great enough combination of capacity and regen that the ship will not rapidly drain its capacity if power drain exceeds normal levels. For example, although very few large ships have regen equal to the power demand of charging a large Jump Drive, their capacity is usually greater than the cost to charge the drive.

A further consideration for larger ships is the use of Power Auxiliaries. These blocks are not more useful than Power Reactor Modules until the latter has reached its peak efficiency (as detailed below, this is approximately 2,000,000 e/sec). After this point, the output of Power Reactor Modules peters out, making way for Power Auxiliaries. They have a similar "soft-cap", but this is per physically separate group, rather than a cap placed on a ship as a whole. However, when a block in a given group of them is destroyed, that group will be affected by a series of explosions, proportional to the size of the affected group. Because of this, they serve as a useful, if risky, way for large ships to further increase power generation.

Power Reactor Rules

Power Reactors have some relatively complex rules governing their power output, especially if one is concerned about efficiency (either in terms of power per block, or power per volume). Two separate formulas are used: one which deals with the output of a single group of reactors (which is only used when the ship has exactly one reactor group), and one which is used to calculate the total output of multiple separate groups on a ship.

Single Group Formula

The formula for a single group of power reactors is as follows:

GroupPower = BlockPower + SizePower

where:

BlockPower = 25 * NumberOfBlocks

and:

SizePower = 2000000 * 2 / ( 1 + 1.000348-0.333*(SumOfDimensions/3)1.7) - 2000000


GroupPower is the sum of the following values.

BlockPower is the base power per second per block of Power Reactors: 25e/sec/block.

SizePower is an extra power value dependent on SumOfDimensions: the sum of dimensions of the minimum bounding box for a given reactor group. SumOfDimensions, of course, is not dependent on aspect ratio: a 3x3x3, 1x1x7, and 2x2x5 bounding box all have a SumOfDimensions of 9. SizePower is of the greatest importance to efficient reactor design as it is an exponential function, and every successive increase in SumOfDimensions has greater value than the last.

Note that SizePower has a maximum value of 2,000,000e/sec, and suffers from diminishing returns as it approaches this value. Also note that for multiple reactor groups, the above formula is modified, and results in a diminishing return to TotalPower. TotalPower of an entity is not the sum of the GroupPower of each group. See the Advanced Analysis section for a more detailed explanation of the equation.

Here are some examples of power reactor groups and how their power outputs are calculated.

  • Example power reactor groups and power values

  • A power reactor by itself has a bounding box with dimensions 1 x 1 x 1.
    SumOfDimensions=3.
    BlockPower=25e.
    SizePower=115e.
    GroupPower=140e.

  • A power reactor group of 3 modules with a bounding box with dimensions 2 x 1 x 2.
    SumOfDimensions=5.
    BlockPower=75e.
    SizePower=276e.
    GroupPower=351e.

  • A power reactor group of 7 modules with a bounding box with dimensions 3 x 3 x 3.
    SumOfDimensions=9.
    BlockPower =175e.
    SizePower=750e.
    GroupPower=925e.

Multiple Group Formula

When there is only one power reactor group on an entity, the GroupPower of that reactor is equal to the total power regen of the entity. However, when there is more than one group, the total power regen of the entity is not the sum of the GroupPower of all groups. Rather, TotalPower of an entity with multiple power reactor groups is subject to diminishing returns, and is given by the following formula:

TotalPower = BlockPower + GroupSumSizePower

where:

BlockPower = 25 * TotalNumberOfBlocksInAllGroups

and:

GroupSumSizePower = 2000000 * 2 / ( 1 + 1.000348-0.333 * GroupSumPower) - 2000000

where:

GroupSumPower = (SumOfDimensionsOfGroup1/3)1.7 + (SumOfDimensionsOfGroup2/3)1.7 ... + (SumOfDimensionsOfGroupn/3)1.7, where n is the number of groups.


To understand the relationship between SizePower, BlockPower and TotalPower, consider a 3x3x3 space in which to place a set of reactor modules. Below are three layouts in this 3x3 space. Note that all values displayed around rounded.

  • Example 3x3x3 layouts with power values

  • A single power reactor group of 27 modules in a 3x3x3 space.
    BlockPower=675e.
    SizePower=750e.
    TotalPower=1425e

  • A single power reactor group of 7 modules in a 3x3x3 space.
    BlockPower=175e.
    SizePower=750e.
    TotalPower=925e.

  • Two power reactor groups of 7 modules each (14 total modules) in a 3x3x3 space.
    BlockPower=350e.
    SizePower=1500e.
    TotalPower=1850e.

Notice that the first and second versions have the same SizePower, as SizePower depends only on the dimensions of the group's bounding box, and not the number of blocks. The first produces more power because it has a greater BlockPower and the same SizePower, but SizePower still contributes more to TotalPower than BlockPower does. Then look at the third version, which has the same dimensions but two groups instead of one. The SizePower is twice that of the other two because there are two groups and because SizePower counts for much more than BlockPower. Because of this, the TotalPower of the third version is much higher than the first one, in spite of having almost half the BlockPower.

Please note that with very small groups as seen above, the diminishing returns of TotalPower with multiple groups is not noticeable due to rounding of such small numbers. However, note the following examples:

  1. 1000 blocks in one group: TotalPower = 1,647,409.7 e/sec
  2. 500 blocks in one group: TotalPower = 683,737.4 e/sec
  3. 1000 total blocks, in two groups of 500: TotalPower = 1,231,567.2 e/sec, not (2*683,737.4=1,367,474.8).

Optimal layouts

None of the examples above are optimal layouts for the cubic 3x3x3 volume, though the third version is close. To create an optimal layout in a given space is rather complex, but it boils down to the following three rules:

  • Maximize the SumOfDimensions for each group, because SizePower is the greatest contributor to TotalPower.
  • Maximize the number of such groups in the space, because this allows you to take advantage of SizePower for each group.
  • Minimize the amount of space not used by reactor groups, without also decreasing the number of groups. It is relevant to note that a 1-block group produces 140e/sec, whereas adding that block to a group without it serving to increase SizePower will only add 25e/sec (from BlockPower) to that group's output.

The optimal layout for the 3x3x3 example above fills in as many spaces as possible in the cube without the two groups touching. By filling in empty spaces of the third example above, we can increase the BlockPower of each group to 250e/s, and we are left with only 7 empty spaces (6 exterior and the block in the middle is omitted). It looks like the following:

  • Optimal 3x3 reactor layout

  • A 3x3 cube with two reactor groups which maximizes the power output in the provided space.
    BlockPower=500e/s.
    SizePower=1499e/s
    TotalPower=1999e/s.

Once the space is well packed with Power Reactor Modules the remaining spaces can be filled with any other module. Bear in mind that blocks which benefit from being in physically contiguous groupings, such as Power Capacitors or Power Auxiliaries do not make ideal fillers, as the gaps between reactors may not be contiguous, depending on reactor layout. Using Shield-Rechargers or Shield Capacitors is common, as they do not rely on being in a group.

Cubic layouts are often non-ideal for a given ship, and are an outdated academic excercize which saw use when these formulas were first being tested. The above 3x3x3 example is the optimal cubic structure, for the most power that can be generated in the given cubic volume, but does not provide the greatest power per second per block (the accepted measure of reactor efficiency) for the 20 blocks used. Reactor layouts should be designed to fit the entity they are built for, in particular to maximise SizePower within the space available.


  • Optimal maximum-output layouts

  • Five reactor groups which maximize the power output for 20 blocks.
    BlockPower=500e/s.
    SizePower=3426.8e/s
    TotalPower=3926.8e/s.

Note that, though not pictured above, a straight line of Power Reactor blocks is also a maximum-efficiency layout for a given block count. This is because each block increases SumOfDimensions, ensuring the greatest possible SizePower for the group.

In the picture above, the first structure on the left uses the same number of blocks as the 3x3x3 cubic power structure shown in the lower middle, but generates almost twice the power at 3926.8e/s. For 20 blocks, this is the maximum power that can be generated. However, other shapes can also achieve the same box dimension sum as the first structure. Each of the other four structures on the upper deck in the picture above also generate the maximum power of 3926.8e/s. Thus it is likely for almost any ship volume that a custom, non-cubic reactor structure will generate more power than simply using a compact cubic reactor. Furthermore, the true cubic volume of all of the structures in the image above is actually 20. In other words, each of the above structures have an identical impact on the internal volume of a given ship, which is to consume 20 blocks of the ship's total internal volume, but the 3x3x3 cubic shape only generates half of the other structure's power per second.

The goal in design of a ship's power generation should be to both maximize every group's box dimensions (netting the greatest power per block efficiency) while also reserving large contiguous volumes within the ship for other systems, as well as rooms of both functional (core room and access paths) and non-functional nature. A cubic volume, although easy to fit into a ship, tends to have a relatively low power per block value, voiding the primary goal of efficient reactor design.

To restate the previously-noted conditions of efficient reactor design:

  • Build the largest optimized group possible within the volume of the ship: ideally, every Power Reactor in the group will increase SumOfDimensions. Simply placing long lines or 3-axes crosses is common, due to the simplicity of the shapes.
    • An allowable exception to this is where a minimal number of redundant (non-SumOfDimensions-increasing blocks) will allow an even greater increase in SumOfDimensions: eg. taking a small detour around other systems to provide a non-negligible increase in SumOfDimensions after the detour.
  • Once the first (and usually largest) group is placed, it is likely that more will be required to reach the desired e/sec output. Where possible, run separate groups along the same path as the primary group, ensuring that you do not connect them at any point (diagonal adjacency is usually preferable). Symmetry may prove useful in placing several groups.
  • Bear in mind that 1-block groups produce 140e/sec, compared to the 25e/sec that redundant blocks in a group will add. Fill gaps with small groups, rather than connecting large groups redundantly; the latter is likely to produce a loss in TotalPower.

There is also a diminishing return to GroupSumSizePower as it approaches 2,000,000e/sec. See the Advanced Analysis section below.


Additional optimal layouts may be found below.

Power Auxiliary Rules

Power Auxiliaries add a new "auxiliary" power pool to a ship, which can be emptied into the main pool for emergency recharging, or used to provide a constant boost to power generation. They should only be used once Power Reactor Modules have reached or surpassed their peak efficiency. They also provide a new element of risk to manage during ship design, as the chain reactions caused by destroying part of a Power Auxiliary group can be significant if not well mitigated.

Main article: Power Auxiliary

Power Capacitor Rules

Power Capacitors have a simpler equation governing their storage capacity, and designing layouts is subsequently vastly simpler.

GroupPower = 1000 * NumBlocks1.05

Unlike Power Reactor Modules, there is no SumOfDimensions value, so the dimensions of the group are irrelevant. All that matters is how many modules are in the group. Since GroupPower is a power function again, the more blocks are in the group the more benefit the group gets from each block. This is called BonusPerBlock below. Thus, for a given number of Power Capacitors is it better to have fewer larger groups than many smaller groups.

Ideally, a ship only has one group of Capacitors. Even if there are necessarily several clumps, they would have a line of capacitors running between them to connect them all into one group.

Here's some sample group sizes and their value breakdowns. Note that values are rounded.

NumBlocks GroupPower BonusPerBlock
1 1,000 0
2 2,071 35
3 3,169 56
4 4,287 72
5 5,419 84
6 6,562 94
7 7,715 102
8 8,877 110
9 10,045 116
10 11,220 122
50 60,802 216
100 125,893 259

Power Reactor Advanced Analysis

This data is mostly of use for builders of large and very large ships. Even though a mid-sized ship might be able to make use of 2 million e/sec, it might not have the internal volume to make an optimized group of 800 or more power reactor modules. However, this analysis does show that small to medium ships should still try to utilize the largest optimized block structures that they can manage within the volume of their ship, as opposed to a higher number of smaller block structures, such as those used in the efficient cube structures.

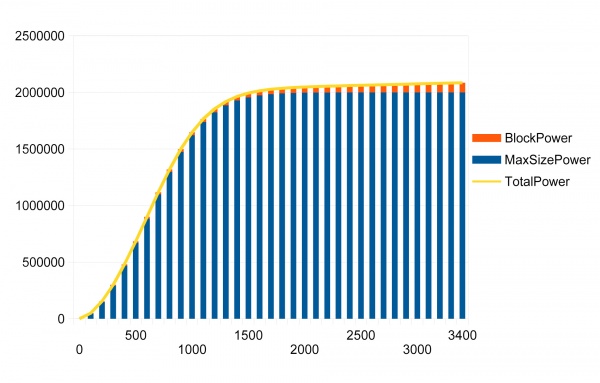
The following table lists the SizePower value generated by an optimal group of blocks of the given number. Note that SizePower does not fully max out at 2,000,000 until the optimized group has 3415 blocks. An optimized group is one with the largest possible box-dimensions for the number of blocks, or a group in which no block fails to increase the box-dimensions of the group:

Blocks Max SizePower BlockPower GroupPower Power/Block Ratio
25 4854.7 625.0 5479.7 219.2
50 14792.4 1250.0 16042.4 320.8
100 46492.6 2500.0 48992.6 489.9
200 148300 5000.0 153300 766.5
300 292236.1 7500.0 299736.1 999.1
400 469724.5 10000.0 479724.5 1199.3
500 671237.4 12500.0 683737.4 1367.5
600 885221.5 15000.0 900221.5 1500.4
700 1098666.6 17500.0 1116166.6 1594.5
800 1298843.6 20000.0 1318843.6 1648.6
895 1467322.0 22375 1489697.0 1664.5
900 1475480.8 22500.0 1497980.8 1664.4
1000 1622409.7 25000.0 1647409.7 1647.4
1100 1738002.7 27500.0 1765502.7 1605.0
1200 1824394.0 30000.0 1854394.0 1545.3
1300 1886032.9 32500.0 1918532.9 1475.8
1400 1928219.9 35000.0 1963219.9 1402.3
1500 1956037.9 37500.0 1993537.9 1329.0
1600 1973774.6 40000.0 2013774.6 1258.6
1700 1984741.6 42500.0 2027241.6 1192.5
1800 1991332.7 45000.0 2036332.7 1131.3
1900 1995189.4 47500.0 2042689.4 1075.1
2000 1997389.4 50000.0 2047389.4 1023.7
2100 1998614.2 52500.0 2051114.2 976.7
2200 1999280.1 55000.0 2054280.1 933.8
2300 1999633.8 57500.0 2057133.8 894.4
2400 1999817.6 60000.0 2059817.6 858.3
2500 1999911.0 62500.0 2062411.0 825.0
2600 1999957.5 65000.0 2064957.5 794.2
2700 1999980.1 67500.0 2067480.1 765.7
2800 1999990.8 70000.0 2069990.8 739.3
2900 1999995.9 72500.0 2072495.9 714.7
3000 1999998.2 75000.0 2074998.2 691.7
3100 1999999.2 77500.0 2077499.2 670.2
3200 1999999.7 80000.0 2079999.7 650.0
3300 1999999.9 82500.0 2082499.9 631.1
3400 1999999.9 85000.0 2084999.9 613.2
3415 2000000.0 85375.0 2085375.0 610.7

The above table is illustrated better in the following chart:

  • Graphs of SizePower and GroupPower per Block

  • SizePower per optimized group of blocks of a given number, and the GroupPower per Block of each group.

It is easy to see that SizePower has diminishing returns after about 900 blocks. The precise number is 895. This is the number of blocks in a group that yields the largest bonus per block, 1664.5, after which it begins to fall. This is due to the S-curve shape of the SizePower graph. Consequently, if building a large ship with thousands of power reactor blocks, it would seem the power system should be composed of optimized groups of about 700 to 1000 blocks each, this range being close enough to 895 that it does not greatly affect the resulting e/sec produced by a large system. However, there is another diminishing return factor applied to multiple groups within a ship. For example, in the chart above a group of 1000 power reactors, optimally, yields 1647409.7.0 e/sec, and a group of 500 power reactors yields 683737.4 e/sec. This has been verified in-game with build 0.199.132. However, using two groups of 500 power reactors does not yield double the 683737.4 e/sec value (i.e 1367474.8), but only 1231567.2 instead. Likewise, 1200 blocks would yield 1854394.0 e/sec, but two groups of 600 only yield 1510422.0 e/sec, not double the 900221.5 e/sec of one group of 600.

This diminishing return factor for groups is a soft limit which effectively limits ships to not much more than 2 million e/sec in practice. Consequently large ships are currently either limited to this value, or else use a docked power module daughter-ship and power drain beams to add more power generation capacity to a base ship.

To get to 2 million e/sec (using optimal layouts with each group):

NumGroups GroupSize TotalBlocks MaxSizePower BlockPower TotalPower Power/Block
1 1528 1528 1961859.7 38250 2000059.7 1308.9
2 983 1966 1975701.3 49150 2000276.3 1017.4
3 758 2274 1981077.4 56850 2000027.4 879.5
4 631 2524 1984801.0 63100 2000576.0 792.6
6 486 2916 1988313.8 72900 2000463.8 686.0
12 311 3732 1993938.6 93300 2001713.6 536.4
18 239 4302 1996248.5 107550 2002223.5 465.4
34 158 5372 2001017.1 134300 2004967.1 373.2
52 119 6188 1999927.0 154700 2002902.0 323.7
94 80 7520 1999194.0 188000 2001194.0 266.1
253 41 10373 2008595.1 259325 2009620.1 193.7

In terms of ship mass, larger groups are more efficient.

Sample Optimized Reactor Layouts

  • Optimal 2x2 and 3x3 reactor layouts

  • A 2x2 cube with two reactor groups.
    BlockPower=125e (100+25)
    SizePower=492e (376+115)
    TotalPower=617e

  • A 3x3 cube with two reactor groups.
    BlockPower=500e (250+250)
    SizePower=1499e (749 + 749)
    TotalPower=1999e

  • Optimal 4x4 reactor layout

  • A 4x4 cube with four reactor groups - layer 1.
    BlockPower=825e (100+200+250+275)
    SizePower=3719e (376+897+1223+1223)
    TotalPower=4544e

  • A 4x4 cube with four reactor groups - layer 2.

  • A 4x4 cube with four reactor groups - layer 3.

  • A 4x4 cube with four reactor groups - layer 4.

  • Optimal 5x5 reactor layout

  • A 5x5 cube with 5 reactor groups.
    BlockPower=1725e (375+375+375+375+225)
    SizePower=8282e (1787+1787+1787+1787+1054)
    TotalPower=9927e

Retrieved from "https://starmadepedia.net/index.php?title=Legacy_Power_Systems&oldid=4069"