Legacy Power Systems

This page describes the power generation and storage mechanisms in StarMade.

Power Generation and Storage Blocks

Power is generated using the Power Reactor Module, though on ships, the Ship Core will generate 1 energy (or e) per second (called e/s) by itself. Planets and Space Stations do not generate any power by themselves. There is a default storage amount of 50,000e on ships, but no default storage for planets and space stations. Power storage can be augmented using Power Capacitors. While these units can be placed anywhere on a ship, planet or station and contribute to either power generation or storage respectively, they are more effective when arranged according to the rules described below. This is particularly important when space is constrained as on most ships.

An important consideration regarding power capacity is that all systems use power from the capacity of a ship or station. If the instantaneous demand for power is not satisfied by the remaining capacity, then the action that is demanding the power will fail to occur. For example, one or all of the missiles that have been commanded to fire will fail to fire due to demanding more power than is currently in storage. However, the power will not be consumed by the failed action. At a minimum, a ship or station should have enough capacity to at least simultaneously fire all the weapon systems attached. Other considerations are the constant demand being made by always-active systems, and how much simultaneous demand will be made when shields begin to recharge, and thrusters need to fire. Power generation is used to refill the power capacity of a ship or station, and needs to be large enough to provide power during sustained demand. Power generation need not equal or exceed all possible demands. For example, charging a jump drive may drain the capacity faster than the power generation can refill it, but as long as the capacity is enough to charge the jump drive without being fully drained, this may be considered to be more than adequate for a given ship.

Power Reactor Rules (Single Group Formula)

Power Reactors have a somewhat complex set of rules associated with them when it comes to creating efficient or compact power systems. This comes from how their power output is calculated, which is not simply by adding up the blocks and multiplying them by some power factor. Instead, the formula for a single group of power reactors is as follows:

GroupPower = BlockPower + SizePower

where:

BlockPower = 25 * NumberOfBlocks

and:

SizePower = 2000000 / ( 1 + 1.000348^{-0.333*(SumOfDimensions/3)1.7}) - 1000000

GroupPower is fairly straightforward, as it is the simple sum of the other two pieces.

BlockPower is the amount of power contributed directly by the Power Reactor Modules in the group, which is just 25e per module.

SizePower is the amount of power contributed by the size of the group, and is only dependent on SumOfDimensions which is the sum of the dimensions of the smallest bounding box which can encompass the entire group. Because SumOfDimensions is a plain sum, a 3x3x3 box, 1x1x7 box and a 2x2x5 box are the same (9) for the purposes of this part of the equation. This is the part of the equation which is most important when considering how to maximize a group of reactors because SizePower is a power function, which means that each successive incremental increase in the value of SumOfDimensions gives much greater benefits than the next lower value.

Note that SizePower caps out at 1,000,000e. Also note that for multiple reactor groups, the above formula is modified, and results in a diminishing return. Total Power of a ship is not the sum of the Group Power of each group. See the Advanced Analysis section for a more detailed explanation of the equation.

Here are some examples of power reactor groups and how their power outputs are calculated.

• Example power reactor groups and power values
• 

  A power reactor by itself has a bounding box with dimensions 1 x 1 x 1.
  SumOfDimensions=3.
  BlockPower=25e.
  SizePower=115e.
  GroupPower=140e.

• 

  A power reactor group of 3 modules with a bounding box with dimensions 2 x 1 x 2.
  SumOfDimensions=5.
  BlockPower=75e.
  SizePower=276e.
  GroupPower=351e.

• 

  A power reactor group of 7 modules with a bounding box with dimensions 3 x 3 x 3.
  SumOfDimensions=9.
  BlockPower =175e.
  SizePower=749e.
  GroupPower=924e.

Relationship between BlockPower, SizePower and TotalPower

When there is only one power reactor block group in or on an entity, the GroupPower and the total power of the entity is identical. However, when there is more than one group, the total power provided to a ship, station or planet is not the sum of the GroupPower of all groups. Rather, TotalPower of an entity with multiple power reactor groups is subject to diminishing returns, and is given by the following formula:

TotalPower = BlockPower + GroupSumSizePower

where:

BlockPower = 25 * TotalNumberOfBlocksInAllGroups

and:

GroupSumSizePower = 2000000 / ( 1 + 1.000348^{-0.333 * GroupSumPower}) - 1000000

where:

GroupSumPower = (SumOfDimensionsOfGroup₁/3)^1.7 + (SumOfDimensionsOfGroup₂/3)^1.7 ... + (SumOfDimensionsOfGroup_n/3)^1.7, where n is the number of groups.

To understand the relationship between SizePower, BlockPower and TotalPower, consider a 3x3 space in which to place a set of reactor modules. Below are three layouts in this 3x3 space. Note that values are rounded which may lead to small apparent discrepancies.

• Example 3x3 layouts with power values
• 3x3Cube.jpg

  A single power reactor group of 27 modules in a 3x3 space.
  BlockPower=675e.
  SizePower=749e.
  TotalPower=1424e

• 3x3SingleEdge.jpg

  A single power reactor group of 7 modules in a 3x3 space.
  BlockPower=175e.
  SizePower=749e.
  TotalPower=924e.

• 3x3DoubleEdge.jpg

  Two power reactor groups of 7 modules each (14 total modules) in a 3x3 space.
  BlockPower=175e each (350e total).
  SizePower=749e each (1499e total).
  TotalPower=1849e.

Notice that the first and second versions have the same SizePower, as SizePower depends only on the dimensions of the group and not the number of blocks. The first of course produces more total power than the second because it has more blocks and each only has a single group, but SizePower still contributes more to the total than the number of blocks does. Then look at the third version, which has the same dimensions but two groups instead of one. The SizePower is twice that of the other two because there are two groups and because SizePower counts for much more than BlockPower the TotalPower of the third version is much higher than the first one, in spite of only having half as many blocks in it (and thus a lower BlockPower).

Please note that with the very small groups in the cubic structure above, the diminishing returns of TotalPower with multiple groups is not noticeable with such small power output rounded to a whole number. But note the case of a group of 1000 power reactors in one group, 500 in one group, and finally a third case of two groups of 500, for a total of 1000 blocks.

1. 1000 in one group: GroupPower/TotalPower = 1003486.0 e/sec
2. 500 in one group: GroupPower/TotalPower = 615706.3 e/sec
3. 1000 in two groups of 500: TotalPower = 909558.9 e/sec, not the sum of 615706.3 twice.

Optimal layouts

None of the examples above are optimal layouts for the cubic 3x3x3 volume, though the third version is getting close. To create an optimal layout in a given space is rather complex, but it boils down to the following three rules:

• Maximize the SumOfDimensions for each group, because this contributes the most to the power equation through SizePower.
• Maximize the number of such groups in the space, because this allows you to take advantage of SizePower for each group
• Minimize the number of empty spaces - that is, spaces which don't contain power reactor modules - without reducing the number of groups. When doing this, be mindful of the fact that a block in a group of its own is worth 140e/s, while a block added to an existing group is only worth 25e/s if it doesn't also add to the physical size of the group.

The optimal layout for the 3x3 example above fills in as many spaces as possible in the cube without the two groups touching. By filling in empty spaces of the third example above, we can increase the BlockPower of each group to 250e/s, and we are left with only 7 empty spaces (6 exterior and the block in the middle is omitted). It looks like the following:

• Optimal 3x3 reactor layout
• 

  A 3x3 cube with two reactor groups which maximizes the power output in the provided space.
  BlockPower=500e/s.
  SizePower=1499e/s
  TotalPower=1999e/s.

Once you have put in as many Power Reactor Modules as you can into the space, you can fill the remaining spaces with any other module, except you should not use Power Capacitors because they can benefit from grouping as well, though it differs from power reactors. Using Shield Rechargers or Shield Capacitors for this purpose is common.

Layouts need not be cube-shaped to be optimal, even though this page uses them for examples. The above 3x3x3 example is the optimal cubic structure, for the most power that can be generated in the smallest cubic volume, but does not provide the most power that can be generated for the blocks used, which is 20. The layout shape will typically be dictated by the ship or station dimensions. Keep in mind that since other shapes provide more power than a cubic volume, it is unlikely that a ship or station would be best served with a perfectly cubic power structure, even if the ship is itself a large cube.

• Optimal maximum-output layouts
• 

  Five reactor groups which maximize the power output for 20 blocks.
  BlockPower=500e/s.
  SizePower=3426.8e/s
  TotalPower=3926.8e/s.

Note that though not pictured above, a simple straight line of Power Reactor blocks is also a maximum-output layout as well.

In the picture above, the first structure on the left uses the same number of cubes as the 3x3x3 cubic power structure shown in the lower middle, but generates almost twice the power at 3926.8e/s. For 20 blocks, this is the maximum power that can be generated. However, other shapes can also achieve the same box dimension sum as the first structure. Each of the other four structures on the upper deck in the picture above also generate the maximum power of 3926.8e/s. Thus it is likely for almost any ship volume that a custom, non-cubic reactor structure will generate more power than simply using an efficient cubic volume. Furthermore, the true cubic volume of all of the structures in the image above is actually 20. In other words, each of the above structures have an identical impact on the internal volume of a given ship, which is to consume 20 blocks of the ship's total internal volume, but the 3x3x3 cubic shape only generates half of the other structure's power per second.

The goal in design of a ship's power generation should be to both maximize the power reactor structure's box dimensions while also reserving large contiguous volumes within the ship for weapons and effects groups, functional areas like a core room, computer room, shuttle docking bay, or cargo hold, and usually some role-play areas, like a cockpit or command deck, medical facility, captain's quarters, corridors, elevators, etc. A cubic volume is not capable of fulfilling this goal.

Taking these things into consideration, the process for designing an optimized power system for a ship is:

1. Build the largest optimized group possible within the volume of the ship. An optimized group is one in which each added power reactor always increases the block dimensions of the group.
2. An allowed exception for the above rule would be, when following the inside of the hull from front to back, it might be necessary to go down before heading back up in order to go further to the back of the ship. (Some of the blocks won't increase the box-dimensions of the group, but they connect and make a contiguous group from front to back, so the group isn't optimal, but it is as close as possible while maximizing contiguous ship volume. Note that if a group consists of 100 blocks, but twenty of these blocks are connector blocks that do not increase the box-dimensions of the group, then this group should be considered as an 80-block system for purposes of calculating its SizePower, as the 20 connector blocks only add 25e/sec each, and do not increase the SizePower efficiency bonus.)
3. Once the first group is laid in, if needing more e/sec, lay in parallel, un-connected groups, extending along the first group as far as possible. In most cases, it is possible to build with symmetry, thus building at least two groups at a time.
4. Finally, even single reactors placed alone, unconnected, will yield 140e/sec, so filling in small pockets with single blocks is better than connecting them to existing groups if they do not also increase the box-dimensions of the group, in which case they only yield 25e/sec.

There is also a diminishing return as the e/sec of a ship approach 1 million e/sec. See the Advanced Analysis section below.

Additional optimal layouts may be found below.

Power Capacitor Rules

Power Capacitors have a simpler equation governing their storage capacity, and designing layouts is subsequently vastly simpler.

GroupPower = 1000 * NumBlocks^1.05

Unlike Power Reactor Modules, there is no SumOfDimensions value, so the dimensions of the group are irrelevant. All that matters is how many modules are in the group. Since GroupPower is a power function again, the more blocks are in the group the more benefit the group gets from each block. This is called BonusPerBlock below. Thus, for a given number of Power Capacitors is it better to have fewer larger groups than many smaller groups.

Ideally, a ship only has one group of Capacitors. Even if there are necessarily several clumps, they would have a line of capacitors running between them to connect them all into one group.

Here's some sample group sizes and their value breakdowns. Note that values are rounded.

NumBlocks	GroupPower	BonusPerBlock
1	1,000	0
2	2,071	35
3	3,169	56
4	4,287	72
5	5,419	84
6	6,562	94
7	7,715	102
8	8,877	110
9	10,045	116
10	11,220	122
50	60,802	216
100	125,893	259

Power Reactor Advanced Analysis

This data is mostly of use for builders of large and very large ships. Even though a mid-sized ship might be able to make use of 1 million e/sec, it might not have the internal volume to make an optimized group of 500 or more power reactor modules. However, this analysis does show that small to medium ships should still try to utilize the largest optimized block structures that they can manage within the volume of their ship, as opposed to a higher number of smaller block structures, such as those used in the efficient cube structures.

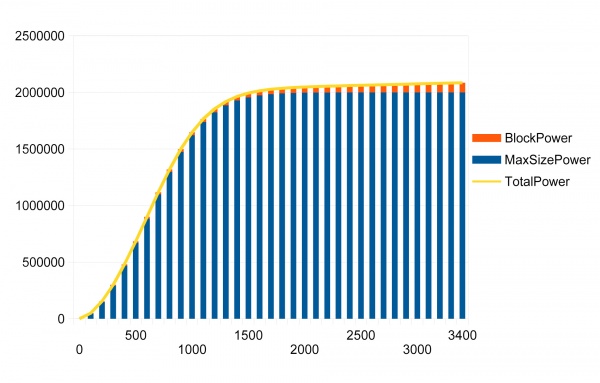
The following table lists the SizePower value generated by an optimal group of blocks of the given number. Note that SizePower does not fully max out at 1,000,000 until the optimized group has 3374 blocks. An optimized group is one with the largest possible box-dimensions for the number of blocks, or a group in which no block fails to increase the box-dimensions of the group:

Blocks	Max SizePower	BlockPower	GroupPower	Power/Block Ratio
25	4853.8	625.0	5478.8	219.2
50	14789.0	1250.0	16039.0	320.8
100	46459.4	2500.0	48959.4	489.6
200	147463.8	5000.0	152463.8	762.3
300	286080.1	7500.0	293580.1	978.6
400	445102.1	10000.0	455102.1	1137.8
500	603206.3	12500.0	615706.3	1231.4
594	732790.3	14850.0	747640.3	1258.7
600	740136.2	15000.0	755136.2	1258.6
700	843919.1	17500.0	861419.1	1230.6
800	913509.0	20000.0	933509.0	1166.9
900	955432.2	22500.0	977932.2	1086.6
1000	978486.0	25000.0	1003486.0	1003.5
1100	990213.8	27500.0	1017713.8	925.2
1200	995787.6	30000.0	1025787.6	854.8
1300	998279.2	32500.0	1030779.2	792.9
1400	999331.5	35000.0	1034331.5	738.8
1500	999752.7	37500.0	1037252.7	691.5
1600	999912.7	40000.0	1039912.7	649.9
1700	999970.6	42500.0	1042470.6	613.2
1800	999990.5	45000.0	1044990.5	580.6
1900	999997.1	47500.0	1047497.1	551.3
2000	999999.1	50000.0	1049999.1	525.0
2100	999999.8	52500.0	1052499.8	501.2
2200	999999.9	55000.0	1054999.9	479.5
2300	1000000.0	57500.0	1057500.0	459.8
2400	1000000.0	60000.0	1060000.0	441.7
2500	1000000.0	62500.0	1062500.0	425.0
2600	1000000.0	65000.0	1065000.0	409.6
2700	1000000.0	67500.0	1067500.0	395.4
2800	1000000.0	70000.0	1070000.0	382.1
2900	1000000.0	72500.0	1072500.0	369.8
3000	1000000.0	75000.0	1075000.0	358.3
3100	1000000.0	77500.0	1077500.0	347.6
3200	1000000.0	80000.0	1080000.0	337.5
3374	1000000.0	84350.0	1084350.0	321.4

The above table is illustrated better in the following chart:

• Graphs of SizePower and GroupPower per Block
• 

  SizePower per optimized group of blocks of a given number, and the GroupPower per Block of each group.

It is easy to see that SizePower has diminishing returns after about 600 blocks. The precise number is 594. This is the number of blocks in a group that yields the largest bonus per block, 1258.7, after which it begins to fall. This is due to the S-curve shape of the SizePower graph. Consequently, if building a large ship with thousands of power reactor blocks, it would seem the power system should be composed of optimized groups of about 500 to 700 blocks each, this range being close enough to 594 that it does not greatly affect the resulting e/sec produced by a large system. However, there is another diminishing return factor applied to multiple groups within a ship. For example, in the chart above a group of 1000 power reactors, optimally, yields 1003486.0 e/sec, and a group of 500 power reactors yields 615706.3 e/sec. This has been verified in-game with build .1867. However, using two groups of 500 power reactors does not yield double the 615706.3 e/sec value, but only 909558.9 instead. Likewise, 1200 blocks would yield 1025787.6 e/sec, but two groups of 600 only yield 986370.9 e/sec, not double the 755136.2 e/sec of one group of 600.

This diminishing return factor for groups is a soft limit which effectively limits ships to not much more than 1 million e/sec in practice. Consequently large ships are currently either limited to this value, or else use a docked power module daughter-ship and power drain beams to add more power generation capacity to a base ship.

To get to 1 million e/sec (using optimal layouts with each group):

NumGroups	GroupSize	TotalBlocks	SumGroupX	MaxSizePower	BlockPower	TotalPower	Power/Block
1	1000	1000	19515.0	978486.0	25000	1003486.0	1003.5
2	700	1400	21315.6	985772.0	35000	1020772.0	729.1
2	650	1300	18799.4	974655.6	32500	1007155.6	774.7
3	500	1500	18080.5	970131.0	37500	1007631.0	671.8
4	400	1600	16524.9	957445.3	40000	997445.3	623.4
6	300	1800	15242.5	943141.8	45000	988141.8	549.0
12	200	2400	15387.7	944970.1	60000	1004970.1	418.7
18	150	2700	14233.1	928695.3	67500	996195.3	369.0
34	100	3400	13645.6	918720.2	85000	1003720.2	295.2
52	75	3900.0	12939.9	904968.8	97500	1002468.8	257.0
94	50	4700.0	12001.3	883230.7	117500	1000730.7	212.9
253	25	6325.0	10600.7	842003.8	158125	1000128.8	158.1

In terms of ship mass, larger groups are more efficient.

Sample Optimized Reactor Layouts

• Optimal 2x2 and 3x3 reactor layouts
• 

  A 2x2 cube with two reactor groups.
  BlockPower=125e (100+25)
  SizePower=492e (376+115)
  TotalPower=617e

• 

  A 3x3 cube with two reactor groups.
  BlockPower=500e (250+250)
  SizePower=1499e (749 + 749)
  TotalPower=1999e

• Optimal 4x4 reactor layout
• 

  A 4x4 cube with four reactor groups - layer 1.
  BlockPower=825e (100+200+250+275)
  SizePower=3719e (376+897+1223+1223)
  TotalPower=4544e

• 

  A 4x4 cube with four reactor groups - layer 2.

• 

  A 4x4 cube with four reactor groups - layer 3.

• 

  A 4x4 cube with four reactor groups - layer 4.

• Optimal 5x5 reactor layout
• 

  A 5x5 cube with 5 reactor groups.
  BlockPower=1725e (375+375+375+375+225)
  SizePower=8282e (1787+1787+1787+1787+1054)
  TotalPower=9927e