Difference between revisions of "Legacy Power Systems"

From StarMade Wiki
(added to the Game Mechanic category)
m (Crimson-Artist moved page Power Systems to Legacy Power Systems: Information on page is outdated)
 
(29 intermediate revisions by 7 users not shown)
Line 1: Line 1:
−
This page describes the power generation and storage mechanisms in '''StarMade'''.
+
{{notig}}
  
 +
'''For information on the current system of power generation in Starmade, see [[Reactors]].'''
 +
 +
This page describes the old, first-run model for power generation and storage mechanisms in '''StarMade''' and is no longer used. Data from this test version was used to design and implement Starmade's current power system, Power 2.0.
 +
 
 
==Power Generation and Storage Blocks==
 
==Power Generation and Storage Blocks==
−
Power is generated using the [[Power Reactor Module]], though on ships, the [[Ship Core]] will generate 1 energy (or e) per second (called e/s) by itself.  [[Planet|Planets]] and [[Space Station|Space Stations]] do not generate any power by themselves. There is a default storage amount of 50,000e on ships, but no default storage for planets and space stations.  Power storage can be augmented using [[Power Capacitor|Power Capacitors]].  While these units can be placed anywhere on a ship, planet or station and contribute to either power generation or storage respectively, they are more effective when arranged according to the rules described below.  This is particularly important when space is constrained as on most ships.
+
Power is generated using either [[Power Reactor Module|Power Reactor Modules]] or [[Power Auxiliary|Power Auxiliaries]], although the latter is greatly preferable as a supplement to the former (when they have reached or surpassed their peak efficiency), not a replacement. Entities built from a [[Ship Core]] have an innate power regen rate of 1 power per second (commonly abbreviated as "e/sec").  [[Planet|Planets]] and [[Space Station|Space Stations]] do not have this innate power generation. Ships also have a base power capacity of 50,000 energy (as with regeneration, planets and stations have no innate power capacity).  Power capacity can be increased using [[Power Capacitor|Power Capacitors]].  All three types of power blocks are more efficient (in terms of power per second per block, or e/sec/block) when placed in particular configurations, as detailed in their sections below.
  
−
An important consideration regarding power capacity is that all systems use power from the '''capacity''' of a ship or station. If the instantaneous demand for power is not satisfied by the remaining capacity, then the action that is demanding the power will fail to occur. For example, one or all of the missiles that have been commanded to fire will fail to fire due to demanding more power than is currently in storage. However, the power will not be consumed by the failed action. At a minimum, a ship or station should have enough capacity to at least simultaneously fire all the weapon systems attached.  Other considerations are the constant demand being made by always-active systems, and how much simultaneous demand will be made when shields begin to recharge, and thrusters need to fire. Power generation is used to refill the power capacity of a ship or station, and needs to be large enough to provide power during sustained demand. Power generation need not equal or exceed all possible demands. For example, charging a jump drive may drain the capacity faster than the power generation can refill it, but as long as the capacity is enough to charge the jump drive without being fully drained, this may be considered to be more than adequate for a given ship.
+
An important consideration is that all systems drain some amount of power from the ship's capacity, either at a constant rate for a period of time (passive effects, scanner and jump drive charging, or cloaking and jamming), or in instantaneous bursts of varying frequency (most weapons). If the instantaneous power cost of an action (eg. firing a large missile) is greater than the power capacity of the ship, the action will not occur, a "Power Failure" warning will appear below the targeting reticle (as well as a red "E" in a triangle, at the top of the screen), and no power will be drained for that action. In most situations, a ship should at least have sufficient capacity to fire one salvo of its alpha (high damage, long cooldown) weapons. Power capacity should usually also include leeway for power spikes caused by shield regeneration costs, thruster activation, and potentially even enemy [[Effects#Offensive_Effects|EMP]] attacks (which can cause significant power drain if the attacking ship is focussed on such weaponry).
  
−
==Power Reactor Rules (Single Group Formula)==
+
Power generation will ideally be greater than the maximum expected rate of power usage: failing this, there should be a great enough combination of capacity and regen that the ship will not rapidly drain its capacity if power drain exceeds normal levels. For example, although very few large ships have regen equal to the power demand of charging a large Jump Drive, their capacity is usually greater than the cost to charge the drive.
−
[[Power Reactor Module|Power Reactors]] have a somewhat complex set of rules associated with them when it comes to creating efficient or compact power systems. This comes from how their power output is calculated, which is not simply by adding up the blocks and multiplying them by some power factor. Instead, the formula for a '''single''' [[Module Group|group]] of power reactors is as follows:
+
 
 +
A further consideration for larger ships is the use of Power Auxiliaries. These blocks are not more useful than Power Reactor Modules until the latter has reached its peak efficiency (as detailed below, this is approximately 2,000,000 e/sec). After this point, the output of Power Reactor Modules peters out, making way for Power Auxiliaries. They have a similar "soft-cap", but this is per physically separate group, rather than a cap placed on a ship as a whole. However, when a block in a given group of them is destroyed, that group will be affected by a series of explosions, proportional to the size of the affected group. Because of this, they serve as a useful, if risky, way for large ships to further increase power generation.
 +
 
 +
==Power Reactor Rules==
 +
[[Power Reactor Module|Power Reactors]] have some relatively complex rules governing their power output, especially if one is concerned about efficiency (either in terms of power per block, or power per volume). Two separate formulas are used: one which deals with the output of a single group of reactors (which is only used when the ship has exactly one reactor group), and one which is used to calculate the total output of multiple separate groups on a ship.
 +
 
 +
===Single Group Formula===
 +
 
 +
The formula for an entity with exactly one Power Reactor group is as follows:
  
 
<tt style="font-size: large">'''GroupPower''' = BlockPower + SizePower</tt>
 
<tt style="font-size: large">'''GroupPower''' = BlockPower + SizePower</tt>
Line 17: Line 29:
 
and:
 
and:
  
−
<tt style="font-size: large">'''SizePower''' = 2000000 / ( 1 + 1.000696<sup>-0.333*(SumOfDimensions/3)<sup>1.7</sup></sup>) - 1000000</tt>
+
<tt style="font-size: large">'''SizePower''' = 2000000 * 2 / ( 1 + 1.000348<sup>-0.333*(SumOfDimensions/3)<sup>1.7</sup></sup>) - 2000000</tt>
  
  
−
'''GroupPower''' is fairly straightforward, as it is the simple sum of the other two pieces.   
+
'''GroupPower''' is the sum of the following values.   
  
−
'''BlockPower''' is the amount of power contributed directly by the [[Power Reactor Module]]s in the group, which is just 25e per module.
+
'''BlockPower''' is the base power per second per block of [[Power Reactor Module|Power Reactors]]: 25e/sec/block.
  
−
'''SizePower''' is the amount of power contributed by the '''size''' of the group, and is only dependent on '''SumOfDimensions''' which is the sum of the dimensions of the smallest bounding box which can encompass the entire group.  Because SumOfDimensions is a plain sum, a 3x3x3 box, 1x1x7 box and a 2x2x5 box are the same (9) for the purposes of this part of the equation.  This is the part of the equation which is most important when considering how to maximize a group of reactors because SizePower is a power function, which means that each successive incremental increase in the value of SumOfDimensions gives much greater benefits than the next lower value.  
+
'''SizePower''' is an extra power value dependent on SumOfDimensions: the sum of dimensions of the minimum bounding box for a given reactor group.  SumOfDimensions, of course, is not dependent on aspect ratio: a 3x3x3, 1x1x7, and 2x2x5 bounding box all have a SumOfDimensions of 9.  SizePower is of the greatest importance to efficient reactor design as it is an exponential function, and every successive increase in SumOfDimensions has greater value than the last.  
  
−
Note that SizePower caps out at 1,000,000e.  Also note that for multiple reactor groups, the above formula is modified, and results in a diminishing return. Total Power of a ship is not the sum of the Group Power of each group. See the [[#Power Reactor Advanced Analysis|Advanced Analysis]] section for a more detailed explanation of the equation.
+
Note that SizePower has a maximum value of 2,000,000e/sec, and suffers from diminishing returns as it approaches this value.  Also note that for multiple reactor groups, the above formula is modified, and results in a diminishing return to TotalPower. TotalPower of an entity is not the sum of the GroupPower of each group. See the Multiple Group Formula below, as well as the [[#Power Reactor Advanced Analysis|Advanced Analysis]] section, for a more detailed explanation of the equation.
  
 
Here are some examples of power reactor groups and how their power outputs are calculated.
 
Here are some examples of power reactor groups and how their power outputs are calculated.
Line 33: Line 45:
 
Image:Bounding Box 1.jpg|A power reactor by itself has a bounding box with dimensions 1 x 1 x 1.<br/>SumOfDimensions=3.<br/>BlockPower=25e.<br/>SizePower=115e.<br/>GroupPower=140e.
 
Image:Bounding Box 1.jpg|A power reactor by itself has a bounding box with dimensions 1 x 1 x 1.<br/>SumOfDimensions=3.<br/>BlockPower=25e.<br/>SizePower=115e.<br/>GroupPower=140e.
 
Image:Bounding Box 2.jpg|A power reactor group of 3 modules with a bounding box with dimensions 2 x 1 x 2.<br/>SumOfDimensions=5.<br/>BlockPower=75e.<br/>SizePower=276e.<br/>GroupPower=351e.
 
Image:Bounding Box 2.jpg|A power reactor group of 3 modules with a bounding box with dimensions 2 x 1 x 2.<br/>SumOfDimensions=5.<br/>BlockPower=75e.<br/>SizePower=276e.<br/>GroupPower=351e.
−
Image:Bounding Box 3.jpg|A power reactor group of 7 modules with a bounding box with dimensions 3 x 3 x 3.<br/>SumOfDimensions=9.<br/>BlockPower =175e.<br/>SizePower=749e.<br/>GroupPower=924e.
+
Image:Bounding Box 3.jpg|A power reactor group of 7 modules with a bounding box with dimensions 3 x 3 x 3.<br/>SumOfDimensions=9.<br/>BlockPower =175e.<br/>SizePower=750e.<br/>GroupPower=925e.
 
</gallery>
 
</gallery>
  
−
===Relationship between BlockPower, SizePower and TotalPower===
+
===Multiple Group Formula===
  
−
When there is only one power reactor block group in or on an entity, the GroupPower and the total power of the entity is identical. However, when there is more than one group, the total power provided to a ship, station or planet is ''not'' the sum of the GroupPower of all groups. Rather,  '''TotalPower''' of an entity with multiple power reactor groups is subject to diminishing returns, and is given by the following formula:
+
When there is only one power reactor group on an entity, the GroupPower of that reactor is equal to the total power regen of the entity. However, when there is more than one group, the total power regen of the entity is ''not'' the sum of the GroupPower of all groups. Rather,  TotalPower of an entity with multiple power reactor groups is subject to diminishing returns, and is given by the following formula:
  
 
<tt style="font-size: large">'''TotalPower''' = BlockPower + GroupSumSizePower</tt>
 
<tt style="font-size: large">'''TotalPower''' = BlockPower + GroupSumSizePower</tt>
Line 48: Line 60:
 
and:
 
and:
  
−
<tt style="font-size: large">'''GroupSumSizePower''' = 2000000 / ( 1 + 1.000696<sup>-0.333 * GroupSumPower</sup>) - 1000000</tt>
+
<tt style="font-size: large">'''GroupSumSizePower''' = 2000000 * 2 / ( 1 + 1.000348<sup>-0.333 * GroupSumPower</sup>) - 2000000</tt>
  
 
where:  
 
where:  
Line 54: Line 66:
 
<tt style="font-size:large">'''GroupSumPower''' = (SumOfDimensionsOfGroup<sub>1</sub>/3)<sup>1.7</sup> + (SumOfDimensionsOfGroup<sub>2</sub>/3)<sup>1.7</sup> ... + (SumOfDimensionsOfGroup<sub>''n''</sub>/3)<sup>1.7</sup></tt>, where ''n'' is the number of groups.
 
<tt style="font-size:large">'''GroupSumPower''' = (SumOfDimensionsOfGroup<sub>1</sub>/3)<sup>1.7</sup> + (SumOfDimensionsOfGroup<sub>2</sub>/3)<sup>1.7</sup> ... + (SumOfDimensionsOfGroup<sub>''n''</sub>/3)<sup>1.7</sup></tt>, where ''n'' is the number of groups.
  
 +
These formulas are displayed on the following [https://www.desmos.com/calculator/9bcasqoi46 Desmos graph].
  
−
To understand the relationship between SizePower, BlockPower and TotalPower, consider a 3x3 space in which to place a set of reactor modules.  Below are three layouts in this 3x3 space.  Note that values are rounded which may lead to small apparent discrepancies.
+
===Optimal Layouts===
−
 
 
−
<gallery mode="traditional" widths=300px heights=300px perrow=3 caption="Example 3x3 layouts with power values">
 
−
Image:3x3Cube.jpg|A single power reactor group of 27 modules in a 3x3 space.<br/>BlockPower=675e.<br/>SizePower=749e.<br/>TotalPower=1424e
 
−
Image:3x3SingleEdge.jpg|A single power reactor group of 7 modules in a 3x3 space.<br/>BlockPower=175e.<br/>SizePower=749e.<br/>TotalPower=924e.
 
−
Image:3x3DoubleEdge.jpg|Two power reactor groups of 7 modules each (14 total modules) in a 3x3 space.<br/>BlockPower=175e each (350e total).<br/>SizePower=749e each (1499e total).<br/>TotalPower=1849e.
 
−
</gallery>
 
−
 
 
−
Notice that the first and second versions have the same SizePower, as SizePower depends only on the dimensions of the group and not the number of blocks.  The first of course produces more total power than the second because it has more blocks and each only has a single group, but SizePower still contributes more to the total than the number of blocks does.  Then look at the third version, which has the same dimensions but two groups instead of one.  The SizePower is twice that of the other two because there are two groups and because SizePower counts for much more than BlockPower the TotalPower of the third version is much higher than the first one, in spite of only having half as many blocks in it (and thus a lower BlockPower).
 
−
 
 
−
Please note that with the very small groups in the cubic structure above, the diminishing returns of TotalPower with multiple groups is not noticeable with such small power output rounded to a whole number.  But note the case of a group of 1000 power reactors in one group, 500 in one group, and finally a third case of two groups of 500, for a total of 1000 blocks.
 
−
 
 
−
# 1000 in one group: GroupPower/TotalPower = 1003486.0 e/sec
 
−
# 500 in one group: GroupPower/TotalPower = 615706.3 e/sec
 
−
# 1000 in two groups of 500: TotalPower = 909558.9 e/sec, not the sum of 615706.3 twice.
 
−
 
 
−
===Optimal layouts===
 
−
None of the examples above are optimal layouts for the cubic 3x3x3 volume, though the third version is getting close.  To create an optimal layout in a given space is rather complex, but it boils down to the following three rules:
 
−
* Maximize the SumOfDimensions for each group, because this contributes the most to the power equation through SizePower.
 
−
* Maximize the number of such groups in the space, because this allows you to take advantage of SizePower for each group
 
−
* Minimize the number of empty spaces - that is, spaces which don't contain power reactor modules - without reducing the number of groups.  When doing this, be mindful of the fact that a block in a group of its own is worth 140e/s, while a block added to an existing group is only worth 25e/s if it doesn't also add to the physical size of the group.
 
−
 
 
−
The optimal layout for the 3x3 example above fills in as many spaces as possible in the cube without the two groups touching.  By filling in empty spaces of the third example above, we can increase the BlockPower of each group to 250e/s, and we are left with only 7 empty spaces (6 exterior and the block in the middle is omitted).  It looks like the following:
 
−
 
 
−
<gallery mode="traditional" widths=300px heights=300px perrow=1 caption="Optimal 3x3 reactor layout">
 
−
Image:3x3Maximized.jpg|A 3x3 cube with two reactor groups which maximizes the power output in the provided space.<br/>BlockPower=500e/s.<br/>SizePower=1499e/s<br/>TotalPower=1999e/s.
 
−
</gallery>
 
−
 
 
−
Once you have put in as many [[Power Reactor Module]]s as you can into the space, you can fill the remaining spaces with any other module, except you should not use [[Power Capacitor]]s because they can benefit from grouping as well, though it differs from power reactors.  Using [[Shield Recharger]]s or [[Shield Capacitor|Shield Capacitors]] for this purpose is common.
 
−
 
 
−
Layouts need not be cube-shaped to be optimal, even though this page uses them for examples.  The above 3x3x3 example is the optimal '''cubic''' structure, for the most power that can be generated in the smallest cubic volume, but does not provide the most power that can be generated for the blocks used, which is 20.  The layout shape will typically be dictated by the ship or station dimensions. Keep in mind that since other shapes provide more power than a cubic volume, it is unlikely that a ship or station would be best served with a perfectly cubic power structure, even if the ship is itself a large cube.
 
−
 
 
  
 
<gallery mode="traditional" widths=900px heights=300px perrow=1 caption="Optimal maximum-output layouts">
 
<gallery mode="traditional" widths=900px heights=300px perrow=1 caption="Optimal maximum-output layouts">
−
Image:OptimalPowerStructures.jpg|Five reactor groups which maximize the power output for 20 blocks.<br/>BlockPower=500e/s.<br/>SizePower=3426.8e/s<br/>TotalPower=3926.8e/s.
+
Image:OptimalPowerStructures.jpg|Background: Five efficient reactor shapes which all maximize the power output for 20 blocks.<br/>Foreground: A "cubic reactor", also 20 blocks: this is an inefficient design in terms of e/sec/block.<br/><br/>Statistics for the 5 efficient reactors:<br/>BlockPower=500e/s.<br/>SizePower=3426.8e/s<br/>TotalPower=3926.8e/s.
 
</gallery>
 
</gallery>
  
−
Note that though not pictured above, a simple straight line of Power Reactor blocks is also a maximum-output layout as well.
+
Every group pictured above (excluding the 3x3x3 "cubic reactor") consists of 20 blocks arranged in an optimal pattern. An optimal pattern for a group is one in which every block increases SumOfDimensions: this of the utmost importance to creating efficient (high power per second per block) reactors. Note that, though not pictured above, a straight line of Power Reactors is also a maximum-efficiency layout for a given block count. This is because each block increases SumOfDimensions, providing the maximum SizePower for the group.
  
−
In the picture above, the first structure on the left uses the same number of cubes as the 3x3x3 cubic power structure shown in the lower middle, but generates almost twice the power at 3926.8e/s. For 20 blocks, this is the maximum power that can be generated. However, other shapes can also achieve the same box dimension sum as the first structure. Each of the other four structures on the upper deck in the picture above '''also''' generate the maximum power of 3926.8e/s. Thus it is likely for almost any ship volume that a custom, non-cubic reactor structure will generate more power than simply using an efficient cubic volume. Furthermore, the true cubic volume of all of the structures in the image above is actually '''20'''. In other words, each of the above structures have an identical impact on the internal volume of a given ship, which is to consume 20 blocks of the ship's total internal volume, but the 3x3x3 cubic shape only generates '''half''' of the other structure's power per second.  
+
The goal in design of a ship's power generation should be to both maximize every group's box dimensions (netting the greatest e/sec/block efficiency) while also reserving large contiguous volumes within the ship for other systems, as well as rooms of both functional (core room and access routes) and non-functional (miscellaneous roleplay/decorative rooms) nature.  
  
−
The goal in design of a ship's power generation should be to both maximize the power reactor structure's box dimensions while also reserving large contiguous volumes within the ship for weapons and effects groups, functional areas like a core room, computer room, shuttle docking bay, or cargo hold, and usually some role-play areas, like a cockpit or command deck, medical facility, captain's quarters, corridors, elevators, etc. A cubic volume is not capable of fulfilling this goal.
+
Outdated "cubic reactors", in which many small groups are tightly packed into a small cubic volume (5x5x5 being particularly common for this type), have a comparatively low e/sec/block value, and are not recommended under any circumstance. They are only an academic excercise, one used when the above formulas were first being uncovered and tested.
  
−
Taking these things into consideration, the process for designing an optimized power system for a ship is:
+
The key points, therefore, of efficient reactor design are:
−
# Build the largest optimized group possible within the volume of the ship. An optimized group is one in which each added power reactor always increases the block dimensions of the group.
+
* For over 9 or more power reactor modules, build the largest optimized single group possible within the volume of the ship, using perpendicular 1-block wide bars. (A single group up to around 1400 to 1800 blocks, or around 2 million e/sec, is about the ideal for large ships). 'Optimized' means that every Power block in the group will increase the SumOfDimensions. Simply placing long straight lines or 3-axis crosses is common, due to the simplicity of the shapes. If the ship is too small to build a single 2-million e/sec reactor, then build a second or third, depending on the volume of the ship and the power desired for that ship.
−
# An allowed exception for the above rule would be, when following the inside of the hull from front to back, it might be necessary to go down before heading back up in order to go further to the back of the ship. (Some of the blocks won't increase the box-dimensions of the group, but they connect and make a contiguous group from front to back, so the group isn't optimal, but it is as close as possible while maximizing contiguous ship volume. Note that if a group consists of 100 blocks, but twenty of these blocks are connector blocks that do not increase the box-dimensions of the group, then this group should be considered as an 80-block system for purposes of calculating its SizePower, as the 20 connector blocks only add 25e/sec each, and do not increase the SizePower efficiency bonus.)
+
** For 8 or fewer power reactor modules, it is optimal to build in disconnected single blocks.
−
# Once the first group is laid in, if needing more e/sec, lay in parallel, un-connected groups, extending along the first group as far as possible. In most cases, it is possible to build with symmetry, thus building at least two groups at a time.
+
** The exceptions to not increasing the Sum-Of-Dimensions of a contiguous block group with every block should only be when taking a detour around other systems or another power block group.
−
# Finally,  even single reactors placed alone, unconnected, will yield 140e/sec, so filling in small pockets with single blocks is better than connecting them to existing groups if they do not also increase the box-dimensions of the group, in which case they only yield 25e/sec.
+
* Once the first (and usually largest) group is placed, it is likely for smaller ships that more groups will be required to reach the desired e/sec output. For medium-sized ships, one group that maximizes the Sum-of-Dimensions within the available volume of the ship will likely not produce as much power as desired. Space permitting, then add in as many more parallel groups which each maximize the sum-of-dimensions within the remaining space.
 +
**Where possible, run separate groups along the same path as the primary group, ensuring that they are not connected face-to-face at any point. Since the first group should have maximized the sum-of-dimensions in the available volume, a parallel group would generally be the best possible shape for the second group, depending on available ship volume.
 +
**Diagonal adjacency (that is to say, adjacent edges, rather than adjacent faces) is normally preferable. This would result in interior block cavities in some cases that could be filled with power-capacitors, for example.
 +
* Bear in mind that 1-block groups produce 140e/sec, compared to the 25e/sec that redundant blocks in a group will add. Therefore, if eking out more power, fill internal spaces with small, separate groups, rather than connecting more blocks to an existing large group, ''redundantly''; the latter is likely to produce significantly less TotalPower for the number of blocks used.
 +
** 'Redundant' in this case means blocks that do not increase the Sum-of-Dimensions.  An 'L' shape is optimal because all blocks each increase the sum-of-dimensions. Making a double-thick 'L' or a hollow square out of the 'L' shape almost doubles the blocks, but results in two sides of the square being all redundant blocks that only contribute 25 e/sec each. Better to make two unconnected 'L' shapes, not a square or double-wide 'L'.
 +
* The power output from Power Reactor Blocks hit peak efficiency at 895 blocks and hit diminishing returns at around 1,200 to 15,00 blocks. Power Auxilaries are are 19.87% more resource intensive to build and usually less efficient.  Once you reach 14,710 Power Reactor blocks in a single group, it becomes economical to, switch to adding groups of 10,000 Power Auxiliary blocks. Power Auxiliary blocks are most efficient in groups of 10,000 (really 9890) blocks.
  
−
There is also a diminishing return as the e/sec of a ship approach 1 million e/sec. See the [[#Power Reactor Advanced Analysis|Advanced Analysis]] section  below.
+
==Power Auxiliary Rules==
−
 
+
Power Auxiliaries add a separate auxiliary power pool to a ship, and gradually refill this over time when off. This pool can be stored up and then emptied into the main power pool for emergency recharging, or if the auxiliaries are left on, they will provide a constant boost to power generation. They should only be used once Power Reactor Modules have reached or surpassed their peak efficiency. They also provide a new element of risk to manage during ship design, as the chain reactions caused by destroying part of a Power Auxiliary group can be significant if not well-mitigated.  
−
 
+
{{main|Power Auxiliary}}
−
Additional optimal layouts may be found [[#Sample optimized reactor layouts|below]].
 
  
 
==Power Capacitor Rules==
 
==Power Capacitor Rules==
−
[[Power Capacitor|Power Capacitors]] have a simpler equation governing their storage capacity, and designing layouts is subsequently vastly simpler.
+
[[Power Capacitor|Power Capacitors]] have a simple exponential equation governing their capacity.
  
 
<tt style="font-size: large">'''GroupPower''' = 1000 * '''NumBlocks'''<sup>1.05</sup></tt>
 
<tt style="font-size: large">'''GroupPower''' = 1000 * '''NumBlocks'''<sup>1.05</sup></tt>
  
−
Unlike [[Power Reactor Module|Power Reactor Modules]], there is no SumOfDimensions value, so the dimensions of the group are irrelevant.  All that matters is how many modules are in the group.  Since '''GroupPower''' is a power function again, the more blocks are in the group the more benefit the group gets from each block.  This is called '''BonusPerBlock''' below.  Thus, for a given number of [[Power Capacitor|Power Capacitors]] is it better to have fewer larger groups than many smaller groups.
+
Note that the only variable is NumBlocks (total block count of the grouping).  Since GroupPower is an exponential function, subsequent blocks provide greater increments than the ones before them.  This increment is labelled "BonusPerBlock" in the table below.  Because of this, the ideal configuration for any number of Power Capacitors is a single physically-contiguous group. Even if there are separate "clumps" or concentrations of blocks, all of these should be connected by thinner lines of capacitors, to ensure maximum output. It is also advisable to have redundant connections between clumps, to avoid the potential for battle damage breaking these connections.
  
−
''Ideally,  a ship only has one group of Capacitors. Even if there are necessarily several clumps, they would have a line of capacitors running between them to connect them all into one group.''
+
Here are some sample group sizes and their value breakdowns.  Note that values are rounded.
−
 
 
−
Here's some sample group sizes and their value breakdowns.  Note that values are rounded.
 
  
 
{|class="wikitable"
 
{|class="wikitable"
Line 150: Line 134:
 
==Power Reactor Advanced Analysis==
 
==Power Reactor Advanced Analysis==
  
−
This data is mostly of use for builders of large and very large ships. Even though a mid-sized ship might be able to make use of 1 million e/sec, it might not have the internal volume to make an optimized group of 500 or more power reactor modules. However, this analysis does show that small to medium ships should still try to utilize the largest optimized block structures that they can manage within the volume of their ship, as opposed to a higher number of smaller block structures, such as those used in the '''efficient cube''' structures.
+
This data is mostly of use for builders of large and very large ships. Even though a mid-sized ship might be able to make use of 2 million e/sec, it might not have the internal volume to make an optimized group of 800 or more power reactor modules. However, this analysis does show that small to medium ships should still try to utilize the largest optimized block structures that they can manage within the volume of their ship: this is always more effective than using outdated "efficient cube" reactor setups.
  
−
The following table lists the SizePower value generated by an optimal group of blocks of the given number. Note that SizePower does not fully max out at 1,000,000 until the optimized group has 3374 blocks. An optimized group is one with the largest possible box-dimensions for the number of blocks, or a group in which no block fails to increase the box-dimensions of the group:
+
The following table lists the SizePower value generated by an optimal group of blocks of the given number. Note that the SizePower formula only [http://www.thefreedictionary.com/asymptotically asymptotically] approaches its maximum value of 2,000,000 e/sec. At 3415 blocks, A one-decimal result rounds to 2 million.
  
 
{|class="wikitable"
 
{|class="wikitable"
 
!Blocks !! Max SizePower !! BlockPower !! GroupPower !! Power/Block Ratio
 
!Blocks !! Max SizePower !! BlockPower !! GroupPower !! Power/Block Ratio
 
|-
 
|-
−
|25||4853.8||625.0||5478.8||219.2
+
|25||4854.7||625.0||5479.7||219.2
 
|-
 
|-
−
|50||14789.0||1250.0||16039.0||320.8
+
|50||14792.4||1250.0||16042.4||320.8
 
|-
 
|-
−
|100||46459.4||2500.0||48959.4||489.6
+
|100||46492.6||2500.0||48992.6||489.9
 
|-
 
|-
−
|200||147463.8||5000.0||152463.8||762.3
+
|200||148300||5000.0||153300||766.5
 
|-
 
|-
−
|300||286080.1||7500.0||293580.1||978.6
+
|300||292236.1||7500.0||299736.1||999.1
 
|-
 
|-
−
|400||445102.1||10000.0||455102.1||1137.8
+
|400||469724.5||10000.0||479724.5||1199.3
 
|-
 
|-
−
|500||603206.3||12500.0||615706.3||1231.4
+
|500||671237.4||12500.0||683737.4||1367.5
 +
|-
 +
|600||885221.5||15000.0||900221.5||1500.4
 +
|-
 +
|700||1098666.6||17500.0||1116166.6||1594.5
 +
|-
 +
|800||1298843.6||20000.0||1318843.6||1648.6
 
|- style="font-style: bold; background-color: green;"
 
|- style="font-style: bold; background-color: green;"
−
|594||732790.3||14850.0||747640.3||1258.7
+
|895||1467322.0||22375||1489697.0||1664.5
 
|-
 
|-
−
|600||740136.2||15000.0||755136.2||1258.6
+
|900||1475480.8||22500.0||1497980.8||1664.4
 
|-
 
|-
−
|700||843919.1||17500.0||861419.1||1230.6
+
|1000||1622409.7||25000.0||1647409.7||1647.4
 
|-
 
|-
−
|800||913509.0||20000.0||933509.0||1166.9
+
|1100||1738002.7||27500.0||1765502.7||1605.0
 
|-
 
|-
−
|900||955432.2||22500.0||977932.2||1086.6
+
|1200||1824394.0||30000.0||1854394.0||1545.3
 
|-
 
|-
−
|1000||978486.0||25000.0||1003486.0||1003.5
+
|1300||1886032.9||32500.0||1918532.9||1475.8
 
|-
 
|-
−
|1100||990213.8||27500.0||1017713.8||925.2
+
|1400||1928219.9||35000.0||1963219.9||1402.3
 
|-
 
|-
−
|1200||995787.6||30000.0||1025787.6||854.8
+
|1500||1956037.9||37500.0||1993537.9||1329.0
 
|-
 
|-
−
|1300||998279.2||32500.0||1030779.2||792.9
+
|1600||1973774.6||40000.0||2013774.6||1258.6
 
|-
 
|-
−
|1400||999331.5||35000.0||1034331.5||738.8
+
|1700||1984741.6||42500.0||2027241.6||1192.5
 
|-
 
|-
−
|1500||999752.7||37500.0||1037252.7||691.5
+
|1800||1991332.7||45000.0||2036332.7||1131.3
 
|-
 
|-
−
|1600||999912.7||40000.0||1039912.7||649.9
+
|1900||1995189.4||47500.0||2042689.4||1075.1
 
|-
 
|-
−
|1700||999970.6||42500.0||1042470.6||613.2
+
|2000||1997389.4||50000.0||2047389.4||1023.7
 
|-
 
|-
−
|1800||999990.5||45000.0||1044990.5||580.6
+
|2100||1998614.2||52500.0||2051114.2||976.7
 
|-
 
|-
−
|1900||999997.1||47500.0||1047497.1||551.3
+
|2200||1999280.1||55000.0||2054280.1||933.8
 
|-
 
|-
−
|2000||999999.1||50000.0||1049999.1||525.0
+
|2300||1999633.8||57500.0||2057133.8||894.4
 
|-
 
|-
−
|2100||999999.8||52500.0||1052499.8||501.2
+
|2400||1999817.6||60000.0||2059817.6||858.3
 
|-
 
|-
−
|2200||999999.9||55000.0||1054999.9||479.5
+
|2500||1999911.0||62500.0||2062411.0||825.0
 
|-
 
|-
−
|2300||1000000.0||57500.0||1057500.0||459.8
+
|2600||1999957.5||65000.0||2064957.5||794.2
 
|-
 
|-
−
|2400||1000000.0||60000.0||1060000.0||441.7
+
|2700||1999980.1||67500.0||2067480.1||765.7
 
|-
 
|-
−
|2500||1000000.0||62500.0||1062500.0||425.0
+
|2800||1999990.8||70000.0||2069990.8||739.3
 
|-
 
|-
−
|2600||1000000.0||65000.0||1065000.0||409.6
+
|2900||1999995.9||72500.0||2072495.9||714.7
 
|-
 
|-
−
|2700||1000000.0||67500.0||1067500.0||395.4
+
|3000||1999998.2||75000.0||2074998.2||691.7
 
|-
 
|-
−
|2800||1000000.0||70000.0||1070000.0||382.1
+
|3100||1999999.2||77500.0||2077499.2||670.2
 
|-
 
|-
−
|2900||1000000.0||72500.0||1072500.0||369.8
+
|3200||1999999.7||80000.0||2079999.7||650.0
 
|-
 
|-
−
|3000||1000000.0||75000.0||1075000.0||358.3
+
|3300||1999999.9||82500.0||2082499.9||631.1
 
|-
 
|-
−
|3100||1000000.0||77500.0||1077500.0||347.6
+
|3400||1999999.9||85000.0||2084999.9||613.2
 
|-
 
|-
−
|3200||1000000.0||80000.0||1080000.0||337.5
+
|3415||2000000.0||85375.0||2085375.0||610.7
−
|-
 
−
|3374||1000000.0||84350.0||1084350.0||321.4
 
 
|}
 
|}
  
−
The above table is illustrated better in the following chart:
+
The above table is illustrated more effectively in the following chart:
  
−
<gallery mode="traditional" widths=600px heights=400px perrow=1 caption="Graphs of SizePower and GroupPower per Block">
+
<gallery mode="traditional" widths=600px heights=400px perrow=1 caption="Graphs of SizePower and Total Power">
−
Image:Max_SizePower_Curve.jpg|SizePower per optimized group of blocks of a given number, and the GroupPower per Block of each group.
+
Image:Max_SizePower_Curve.jpg|SizePower per optimized group of blocks of a given number.
 
</gallery>
 
</gallery>
  
−
It is easy to see that SizePower has diminishing returns after about 600 blocks. The precise number is 594. This is the number of blocks in a group that yields the largest bonus per block, 1258.7, after which it begins to fall. This is due to the S-curve shape of the SizePower graph. Consequently, if building a large ship with thousands of power reactor blocks, ''it would seem'' the power system should be composed of optimized groups of about 500 to 700 blocks each, this range being close enough to 594 that it does not greatly affect the resulting e/sec produced by a large system. However, there is another diminishing return factor applied to multiple groups within a ship. For example, in the chart above a group of 1000 power reactors, optimally, yields 1003486.0 e/sec, and a group of 500 power reactors yields 615706.3 e/sec. This has been verified in-game with build '''.1867'''. However, using two groups of 500 power reactors does not yield double the 615706.3 e/sec value, but only 909558.9 instead. Likewise, 1200 blocks would yield 1025787.6 e/sec, but two groups of 600 only yield 986370.9 e/sec, not double the 755136.2 e/sec of one group of 600.
+
It is easy to see that SizePower has diminishing returns after about 900 blocks. The precise number is 895. This is the number of blocks in a group that yields the maximum GroupPower per block, 1664.5, after which it begins to fall. If the groups were simply summed, then the ideal ship would have a couple of groups of about 895 blocks, or so. However, since the group formula introduces diminishing returns for multiple groups, it is best to use as few groups as possible, preferably one, if ship size permits.
−
 
+
The asymptotic limit for SizePower at 2 million effectively soft-limits the number of blocks to around 1600-1800 due to diminishing returns. This effectively limits efficient ship power to around 2 million e/sec or so, in practice. The extra e/sec is not worth the doubling of power blocks to 3400 from around 1700 to gain a mere 50K. In fact, it might be better to roughly limit at around 1400 blocks or less. The first 400 blocks adds 469K e/sec to a ship. The last 400 blocks, from 1400 to 1800, only adds only about 73K e/sec. Consequently, large ships might be better served using those hundreds of blocks (or thousands if considering a higher +3K limit) in an [[Power Auxiliary]] system.  
−
This diminishing return factor for groups is a soft limit which effectively limits ships to not much more than 1 million e/sec in practice. Consequently large ships are currently either limited to this value, or else use a ''docked '''power module''' daughter-ship'' and power drain beams to add more power generation capacity to a base ship.  
 
  
−
To get to 1 million e/sec (using optimal layouts with each group):
+
The table below illustrates the diminishing returns of multiple groups.
 +
To get to 2 million e/sec (using optimal layouts with each group):
 
{|class="wikitable"
 
{|class="wikitable"
−
!NumGroups!!GroupSize!!TotalBlocks!!SumGroupX!!MaxSizePower!!BlockPower!!TotalPower!!Power/Block
+
!NumGroups!!GroupSize!!TotalBlocks!!MaxSizePower!!BlockPower!!TotalPower!!Power/Block
−
|-
 
−
|1||1000||1000||19515.0||978486.0||25000||1003486.0||1003.5
 
 
|-
 
|-
−
|2||700||1400||21315.6||985772.0||35000||1020772.0||729.1
+
|1||1528||1528||1961859.7||38250||2000059.7||1308.9
 
|-
 
|-
−
|2||650||1300||18799.4||974655.6||32500||1007155.6||774.7
+
|2||983||1966||1975701.3||49150||2000276.3||1017.4
 
|-
 
|-
−
|3||500||1500||18080.5||970131.0||37500||1007631.0||671.8
+
|3||758||2274||1981077.4||56850||2000027.4||879.5
 
|-
 
|-
−
|4||400||1600||16524.9||957445.3||40000||997445.3||623.4
+
|4||631||2524||1984801.0||63100||2000576.0||792.6
 
|-
 
|-
−
|6||300||1800||15242.5||943141.8||45000||988141.8||549.0
+
|6||486||2916||1988313.8||72900||2000463.8||686.0
 
|-
 
|-
−
|12||200||2400||15387.7||944970.1||60000||1004970.1||418.7
+
|12||311||3732||1993938.6||93300||2001713.6||536.4
 
|-
 
|-
−
|18||150||2700||14233.1||928695.3||67500||996195.3||369.0
+
|18||239||4302||1996248.5||107550||2002223.5||465.4
 
|-
 
|-
−
|34||100||3400||13645.6||918720.2||85000||1003720.2||295.2
+
|34||158||5372||2001017.1||134300||2004967.1||373.2
 
|-
 
|-
−
|52||75||3900.0||12939.9||904968.8||97500||1002468.8||257.0
+
|52||119||6188||1999927.0||154700||2002902.0||323.7
 
|-
 
|-
−
|94||50||4700.0||12001.3||883230.7||117500||1000730.7||212.9
+
|94||80||7520||1999194.0||188000||2001194.0||266.1
 
|-
 
|-
−
|253||25||6325.0||10600.7||842003.8||158125||1000128.8||158.1
+
|253||41||10373||2008595.1||259325||2009620.1||193.7
 
|}
 
|}
−
 
+
==Related==
−
In terms of ship mass, larger groups are more efficient.
+
{{Game Mechanics Navigator}}
−
 
 
−
==Sample Optimized Reactor Layouts==
 
−
 
 
−
<gallery mode="traditional" widths=300px heights=300px perrow=2 caption="Optimal 2x2 and 3x3 reactor layouts">
 
−
Image:2x2Maximized.jpg|A 2x2 cube with two reactor groups.<br/>BlockPower=125e (100+25)<br/>SizePower=492e (376+115)<br/>TotalPower=617e
 
−
Image:3x3Maximized.jpg|A 3x3 cube with two reactor groups.<br/>BlockPower=500e (250+250)<br/>SizePower=1499e (749 + 749)<br/>TotalPower=1999e
 
−
</gallery>
 
−
 
 
−
<gallery mode="traditional" widths=300px heights=300px perrow=4 caption="Optimal 4x4 reactor layout">
 
−
Image:4x4MaximizedLayer1.jpg|A 4x4 cube with four reactor groups - layer 1.<br/>BlockPower=825e (100+200+250+275)<br/>SizePower=3719e (376+897+1223+1223)<br/>TotalPower=4544e
 
−
Image:4x4MaximizedLayer2.jpg|A 4x4 cube with four reactor groups - layer 2.
 
−
Image:4x4MaximizedLayer3.jpg|A 4x4 cube with four reactor groups - layer 3.
 
−
Image:4x4MaximizedLayer4.jpg|A 4x4 cube with four reactor groups - layer 4.
 
−
</gallery>
 
−
 
 
−
<gallery mode="traditional" widths=1000px heights=200px  perrow=1 caption="Optimal 5x5 reactor layout">
 
−
Image:Power Block Compact.png|A 5x5 cube with 5 reactor groups.<br/>BlockPower=1725e (375+375+375+375+225)<br/>SizePower=8282e (1787+1787+1787+1787+1054)<br/>TotalPower=9927e
 
−
</gallery>
 
−
 
 
 
[[Category:Articles]]
 
[[Category:Articles]]
 
[[Category:Game Mechanics]]
 
[[Category:Game Mechanics]]

Latest revision as of 00:35, 6 May 2018

 Legacy Power Systems is no longer in-game.
Information on this page is no longer relevant in-game documentation in current versions of StarMade. The page Legacy Power Systems is for historical purposes only.

For information on the current system of power generation in Starmade, see Reactors.

This page describes the old, first-run model for power generation and storage mechanisms in StarMade and is no longer used. Data from this test version was used to design and implement Starmade's current power system, Power 2.0.

Power Generation and Storage Blocks

Power is generated using either Power Reactor Modules or Power Auxiliaries, although the latter is greatly preferable as a supplement to the former (when they have reached or surpassed their peak efficiency), not a replacement. Entities built from a Ship Core have an innate power regen rate of 1 power per second (commonly abbreviated as "e/sec"). Planets and Space Stations do not have this innate power generation. Ships also have a base power capacity of 50,000 energy (as with regeneration, planets and stations have no innate power capacity). Power capacity can be increased using Power Capacitors. All three types of power blocks are more efficient (in terms of power per second per block, or e/sec/block) when placed in particular configurations, as detailed in their sections below.

An important consideration is that all systems drain some amount of power from the ship's capacity, either at a constant rate for a period of time (passive effects, scanner and jump drive charging, or cloaking and jamming), or in instantaneous bursts of varying frequency (most weapons). If the instantaneous power cost of an action (eg. firing a large missile) is greater than the power capacity of the ship, the action will not occur, a "Power Failure" warning will appear below the targeting reticle (as well as a red "E" in a triangle, at the top of the screen), and no power will be drained for that action. In most situations, a ship should at least have sufficient capacity to fire one salvo of its alpha (high damage, long cooldown) weapons. Power capacity should usually also include leeway for power spikes caused by shield regeneration costs, thruster activation, and potentially even enemy EMP attacks (which can cause significant power drain if the attacking ship is focussed on such weaponry).

Power generation will ideally be greater than the maximum expected rate of power usage: failing this, there should be a great enough combination of capacity and regen that the ship will not rapidly drain its capacity if power drain exceeds normal levels. For example, although very few large ships have regen equal to the power demand of charging a large Jump Drive, their capacity is usually greater than the cost to charge the drive.

A further consideration for larger ships is the use of Power Auxiliaries. These blocks are not more useful than Power Reactor Modules until the latter has reached its peak efficiency (as detailed below, this is approximately 2,000,000 e/sec). After this point, the output of Power Reactor Modules peters out, making way for Power Auxiliaries. They have a similar "soft-cap", but this is per physically separate group, rather than a cap placed on a ship as a whole. However, when a block in a given group of them is destroyed, that group will be affected by a series of explosions, proportional to the size of the affected group. Because of this, they serve as a useful, if risky, way for large ships to further increase power generation.

Power Reactor Rules

Power Reactors have some relatively complex rules governing their power output, especially if one is concerned about efficiency (either in terms of power per block, or power per volume). Two separate formulas are used: one which deals with the output of a single group of reactors (which is only used when the ship has exactly one reactor group), and one which is used to calculate the total output of multiple separate groups on a ship.

Single Group Formula

The formula for an entity with exactly one Power Reactor group is as follows:

GroupPower = BlockPower + SizePower

where:

BlockPower = 25 * NumberOfBlocks

and:

SizePower = 2000000 * 2 / ( 1 + 1.000348-0.333*(SumOfDimensions/3)1.7) - 2000000


GroupPower is the sum of the following values.

BlockPower is the base power per second per block of Power Reactors: 25e/sec/block.

SizePower is an extra power value dependent on SumOfDimensions: the sum of dimensions of the minimum bounding box for a given reactor group. SumOfDimensions, of course, is not dependent on aspect ratio: a 3x3x3, 1x1x7, and 2x2x5 bounding box all have a SumOfDimensions of 9. SizePower is of the greatest importance to efficient reactor design as it is an exponential function, and every successive increase in SumOfDimensions has greater value than the last.

Note that SizePower has a maximum value of 2,000,000e/sec, and suffers from diminishing returns as it approaches this value. Also note that for multiple reactor groups, the above formula is modified, and results in a diminishing return to TotalPower. TotalPower of an entity is not the sum of the GroupPower of each group. See the Multiple Group Formula below, as well as the Advanced Analysis section, for a more detailed explanation of the equation.

Here are some examples of power reactor groups and how their power outputs are calculated.

  • Example power reactor groups and power values

  • A power reactor by itself has a bounding box with dimensions 1 x 1 x 1.
    SumOfDimensions=3.
    BlockPower=25e.
    SizePower=115e.
    GroupPower=140e.

  • A power reactor group of 3 modules with a bounding box with dimensions 2 x 1 x 2.
    SumOfDimensions=5.
    BlockPower=75e.
    SizePower=276e.
    GroupPower=351e.

  • A power reactor group of 7 modules with a bounding box with dimensions 3 x 3 x 3.
    SumOfDimensions=9.
    BlockPower =175e.
    SizePower=750e.
    GroupPower=925e.

Multiple Group Formula

When there is only one power reactor group on an entity, the GroupPower of that reactor is equal to the total power regen of the entity. However, when there is more than one group, the total power regen of the entity is not the sum of the GroupPower of all groups. Rather, TotalPower of an entity with multiple power reactor groups is subject to diminishing returns, and is given by the following formula:

TotalPower = BlockPower + GroupSumSizePower

where:

BlockPower = 25 * TotalNumberOfBlocksInAllGroups

and:

GroupSumSizePower = 2000000 * 2 / ( 1 + 1.000348-0.333 * GroupSumPower) - 2000000

where:

GroupSumPower = (SumOfDimensionsOfGroup1/3)1.7 + (SumOfDimensionsOfGroup2/3)1.7 ... + (SumOfDimensionsOfGroupn/3)1.7, where n is the number of groups.

These formulas are displayed on the following Desmos graph.

Optimal Layouts

  • Optimal maximum-output layouts

  • Background: Five efficient reactor shapes which all maximize the power output for 20 blocks.
    Foreground: A "cubic reactor", also 20 blocks: this is an inefficient design in terms of e/sec/block.

    Statistics for the 5 efficient reactors:
    BlockPower=500e/s.
    SizePower=3426.8e/s
    TotalPower=3926.8e/s.

Every group pictured above (excluding the 3x3x3 "cubic reactor") consists of 20 blocks arranged in an optimal pattern. An optimal pattern for a group is one in which every block increases SumOfDimensions: this of the utmost importance to creating efficient (high power per second per block) reactors. Note that, though not pictured above, a straight line of Power Reactors is also a maximum-efficiency layout for a given block count. This is because each block increases SumOfDimensions, providing the maximum SizePower for the group.

The goal in design of a ship's power generation should be to both maximize every group's box dimensions (netting the greatest e/sec/block efficiency) while also reserving large contiguous volumes within the ship for other systems, as well as rooms of both functional (core room and access routes) and non-functional (miscellaneous roleplay/decorative rooms) nature.

Outdated "cubic reactors", in which many small groups are tightly packed into a small cubic volume (5x5x5 being particularly common for this type), have a comparatively low e/sec/block value, and are not recommended under any circumstance. They are only an academic excercise, one used when the above formulas were first being uncovered and tested.

The key points, therefore, of efficient reactor design are:

  • For over 9 or more power reactor modules, build the largest optimized single group possible within the volume of the ship, using perpendicular 1-block wide bars. (A single group up to around 1400 to 1800 blocks, or around 2 million e/sec, is about the ideal for large ships). 'Optimized' means that every Power block in the group will increase the SumOfDimensions. Simply placing long straight lines or 3-axis crosses is common, due to the simplicity of the shapes. If the ship is too small to build a single 2-million e/sec reactor, then build a second or third, depending on the volume of the ship and the power desired for that ship.
    • For 8 or fewer power reactor modules, it is optimal to build in disconnected single blocks.
    • The exceptions to not increasing the Sum-Of-Dimensions of a contiguous block group with every block should only be when taking a detour around other systems or another power block group.
  • Once the first (and usually largest) group is placed, it is likely for smaller ships that more groups will be required to reach the desired e/sec output. For medium-sized ships, one group that maximizes the Sum-of-Dimensions within the available volume of the ship will likely not produce as much power as desired. Space permitting, then add in as many more parallel groups which each maximize the sum-of-dimensions within the remaining space.
    • Where possible, run separate groups along the same path as the primary group, ensuring that they are not connected face-to-face at any point. Since the first group should have maximized the sum-of-dimensions in the available volume, a parallel group would generally be the best possible shape for the second group, depending on available ship volume.
    • Diagonal adjacency (that is to say, adjacent edges, rather than adjacent faces) is normally preferable. This would result in interior block cavities in some cases that could be filled with power-capacitors, for example.
  • Bear in mind that 1-block groups produce 140e/sec, compared to the 25e/sec that redundant blocks in a group will add. Therefore, if eking out more power, fill internal spaces with small, separate groups, rather than connecting more blocks to an existing large group, redundantly; the latter is likely to produce significantly less TotalPower for the number of blocks used.
    • 'Redundant' in this case means blocks that do not increase the Sum-of-Dimensions. An 'L' shape is optimal because all blocks each increase the sum-of-dimensions. Making a double-thick 'L' or a hollow square out of the 'L' shape almost doubles the blocks, but results in two sides of the square being all redundant blocks that only contribute 25 e/sec each. Better to make two unconnected 'L' shapes, not a square or double-wide 'L'.
  • The power output from Power Reactor Blocks hit peak efficiency at 895 blocks and hit diminishing returns at around 1,200 to 15,00 blocks. Power Auxilaries are are 19.87% more resource intensive to build and usually less efficient. Once you reach 14,710 Power Reactor blocks in a single group, it becomes economical to, switch to adding groups of 10,000 Power Auxiliary blocks. Power Auxiliary blocks are most efficient in groups of 10,000 (really 9890) blocks.

Power Auxiliary Rules

Power Auxiliaries add a separate auxiliary power pool to a ship, and gradually refill this over time when off. This pool can be stored up and then emptied into the main power pool for emergency recharging, or if the auxiliaries are left on, they will provide a constant boost to power generation. They should only be used once Power Reactor Modules have reached or surpassed their peak efficiency. They also provide a new element of risk to manage during ship design, as the chain reactions caused by destroying part of a Power Auxiliary group can be significant if not well-mitigated.

Main article: Power Auxiliary

Power Capacitor Rules

Power Capacitors have a simple exponential equation governing their capacity.

GroupPower = 1000 * NumBlocks1.05

Note that the only variable is NumBlocks (total block count of the grouping). Since GroupPower is an exponential function, subsequent blocks provide greater increments than the ones before them. This increment is labelled "BonusPerBlock" in the table below. Because of this, the ideal configuration for any number of Power Capacitors is a single physically-contiguous group. Even if there are separate "clumps" or concentrations of blocks, all of these should be connected by thinner lines of capacitors, to ensure maximum output. It is also advisable to have redundant connections between clumps, to avoid the potential for battle damage breaking these connections.

Here are some sample group sizes and their value breakdowns. Note that values are rounded.

NumBlocks GroupPower BonusPerBlock
1 1,000 0
2 2,071 35
3 3,169 56
4 4,287 72
5 5,419 84
6 6,562 94
7 7,715 102
8 8,877 110
9 10,045 116
10 11,220 122
50 60,802 216
100 125,893 259

Power Reactor Advanced Analysis

This data is mostly of use for builders of large and very large ships. Even though a mid-sized ship might be able to make use of 2 million e/sec, it might not have the internal volume to make an optimized group of 800 or more power reactor modules. However, this analysis does show that small to medium ships should still try to utilize the largest optimized block structures that they can manage within the volume of their ship: this is always more effective than using outdated "efficient cube" reactor setups.

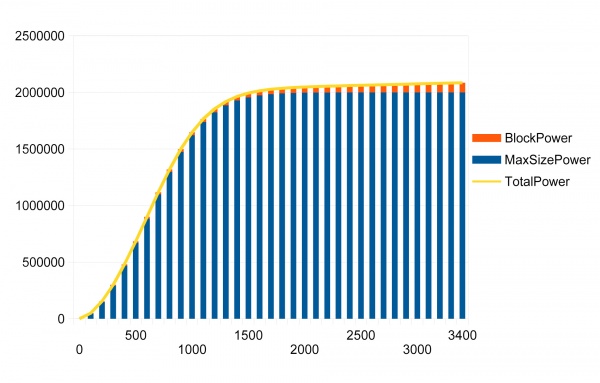
The following table lists the SizePower value generated by an optimal group of blocks of the given number. Note that the SizePower formula only asymptotically approaches its maximum value of 2,000,000 e/sec. At 3415 blocks, A one-decimal result rounds to 2 million.

Blocks Max SizePower BlockPower GroupPower Power/Block Ratio
25 4854.7 625.0 5479.7 219.2
50 14792.4 1250.0 16042.4 320.8
100 46492.6 2500.0 48992.6 489.9
200 148300 5000.0 153300 766.5
300 292236.1 7500.0 299736.1 999.1
400 469724.5 10000.0 479724.5 1199.3
500 671237.4 12500.0 683737.4 1367.5
600 885221.5 15000.0 900221.5 1500.4
700 1098666.6 17500.0 1116166.6 1594.5
800 1298843.6 20000.0 1318843.6 1648.6
895 1467322.0 22375 1489697.0 1664.5
900 1475480.8 22500.0 1497980.8 1664.4
1000 1622409.7 25000.0 1647409.7 1647.4
1100 1738002.7 27500.0 1765502.7 1605.0
1200 1824394.0 30000.0 1854394.0 1545.3
1300 1886032.9 32500.0 1918532.9 1475.8
1400 1928219.9 35000.0 1963219.9 1402.3
1500 1956037.9 37500.0 1993537.9 1329.0
1600 1973774.6 40000.0 2013774.6 1258.6
1700 1984741.6 42500.0 2027241.6 1192.5
1800 1991332.7 45000.0 2036332.7 1131.3
1900 1995189.4 47500.0 2042689.4 1075.1
2000 1997389.4 50000.0 2047389.4 1023.7
2100 1998614.2 52500.0 2051114.2 976.7
2200 1999280.1 55000.0 2054280.1 933.8
2300 1999633.8 57500.0 2057133.8 894.4
2400 1999817.6 60000.0 2059817.6 858.3
2500 1999911.0 62500.0 2062411.0 825.0
2600 1999957.5 65000.0 2064957.5 794.2
2700 1999980.1 67500.0 2067480.1 765.7
2800 1999990.8 70000.0 2069990.8 739.3
2900 1999995.9 72500.0 2072495.9 714.7
3000 1999998.2 75000.0 2074998.2 691.7
3100 1999999.2 77500.0 2077499.2 670.2
3200 1999999.7 80000.0 2079999.7 650.0
3300 1999999.9 82500.0 2082499.9 631.1
3400 1999999.9 85000.0 2084999.9 613.2
3415 2000000.0 85375.0 2085375.0 610.7

The above table is illustrated more effectively in the following chart:

  • Graphs of SizePower and Total Power

  • SizePower per optimized group of blocks of a given number.

It is easy to see that SizePower has diminishing returns after about 900 blocks. The precise number is 895. This is the number of blocks in a group that yields the maximum GroupPower per block, 1664.5, after which it begins to fall. If the groups were simply summed, then the ideal ship would have a couple of groups of about 895 blocks, or so. However, since the group formula introduces diminishing returns for multiple groups, it is best to use as few groups as possible, preferably one, if ship size permits. The asymptotic limit for SizePower at 2 million effectively soft-limits the number of blocks to around 1600-1800 due to diminishing returns. This effectively limits efficient ship power to around 2 million e/sec or so, in practice. The extra e/sec is not worth the doubling of power blocks to 3400 from around 1700 to gain a mere 50K. In fact, it might be better to roughly limit at around 1400 blocks or less. The first 400 blocks adds 469K e/sec to a ship. The last 400 blocks, from 1400 to 1800, only adds only about 73K e/sec. Consequently, large ships might be better served using those hundreds of blocks (or thousands if considering a higher +3K limit) in an Power Auxiliary system.

The table below illustrates the diminishing returns of multiple groups. To get to 2 million e/sec (using optimal layouts with each group):

NumGroups GroupSize TotalBlocks MaxSizePower BlockPower TotalPower Power/Block
1 1528 1528 1961859.7 38250 2000059.7 1308.9
2 983 1966 1975701.3 49150 2000276.3 1017.4
3 758 2274 1981077.4 56850 2000027.4 879.5
4 631 2524 1984801.0 63100 2000576.0 792.6
6 486 2916 1988313.8 72900 2000463.8 686.0
12 311 3732 1993938.6 93300 2001713.6 536.4
18 239 4302 1996248.5 107550 2002223.5 465.4
34 158 5372 2001017.1 134300 2004967.1 373.2
52 119 6188 1999927.0 154700 2002902.0 323.7
94 80 7520 1999194.0 188000 2001194.0 266.1
253 41 10373 2008595.1 259325 2009620.1 193.7

Related

Game Mechanics
Build Mode • Credit • Defense Systems • Docking/Rails • Doors • Effects • Faction • Fleets • Flight Mode • Linking • Logic Signals • Map • Player • Player Items • Production • Propulsion Systems • Reactors • Reactor Chambers • Resources • Shipyards • Shops • Space Station • Support Tool Systems • Trade Network • Warp Gate • Weapons
Retrieved from "https://starmadepedia.net/index.php?title=Legacy_Power_Systems&oldid=6451"